Harvest Imaging Blog

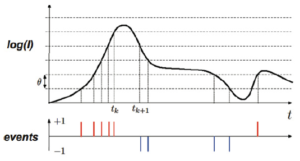
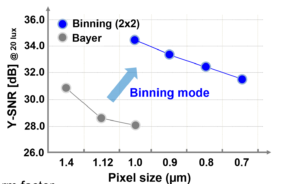
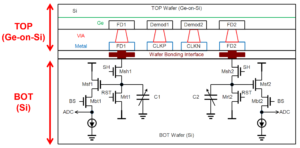
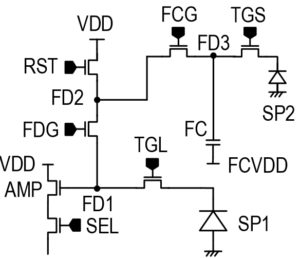
During the last days of 2023, it is again an interesting moment to look back over the last 12 months.  Many things have changed in the world, unfortunately not only for the better.  It is really sad to report that the military imaging business is booming due to the many deadly conflicts humanity is facing.  It would be great to know that the businesses are booming because of other reasons.  Despite the fact that not everyone is living in a peaceful world, it is time to overlook the work of Harvest Imaging in 2023.

Harvest Imaging has 4 major pilars on which the business is relying :

1. the training and teaching in the field of solid-state image capturing.  This part of the Harvest Imaging services is still going strong.  Many existing customers are asking for more and more training, several new customers are added.  It is really remarkable how many different application fields are requiring training.  Because I have seen in the past a lot of airports, a lot of hotels, because I have enjoyed a lot of airplane food, I decided to run most trainings on-line.  Overseas travelling, jet lag and teaching for 6 to 8 hours per day in front of professionals is not the optimum combination.  I am thankful towards my customers that they do understand this.  The training agenda for 2024 is almost completely booked, even a couple of courses are already scheduled for 2025,
2. consulting.  I decided to slow down in consulting activities, and this is done by no longer accepting new customers.  Sometimes it is very difficult to say “no”, but at a particular time in life, working loads have to be reduced,
3. technical projects : these are projects I define myself, with no deadlines and even less pressure.  In 2023 a very interesting project on noise in an existing device was started : how to explain a specific noise pattern in the dark output image of a CIS.  As mentioned already many times : doing measurements and experiments yourself is the best learning school for an image sensor engineer !
4. Harvest Imaging Forum : this hybrid event was again successful in 2023 when the topic focused on “Imaging outside the Visible Spectrum”.  Most probably the 2024 version of the forum will be limited to an in-person event.

Besides the activities of Harvest Imaging, in 2023 I still had my part-time assignment at the Delft University of Technology, but this came to an end in May 2023.  I still have to make sure that also my last two PhD students will defend their thesis, but all practical work in Delft is finished (at least for me).  My successor, Padmakumar Rao, took over the academic activities.

What about 2024 ?  For sure the training and teaching part of Harvest Imaging will continue.  Also the preparations for an extra Harvest Imaging forum have started.  Both activities allow me to stay in touch with the imaging community that brought me a lot of joy since 1976 when I stepped into imaging.

Finally, it is a pleasure for me to wish all my customers and readers a great Christmas period and a Happy, Healthy and Peaceful 2024.

Albert.

On Monday, 20 February, I attended the Image Sensor Session at ISSCC 2023. It provided over eight talks and interesting mix of presentations. The most noticeable change with this year’s session was the large presence of event-driven image sensors versus the single presentations each on SPAD-based and on small pixel mobile devices. The other presentations described a silicon-based terahertz image sensor, an x-ray image sensor and a low-power image sensor powered with on-chip energy harvesting.

The first two talks described image sensors that integrated both event-driven and standard CIS pixels within the same pixel array to allow high speed acquisition of changes in the scene interleaved with full-color video. This allowed the creation of high speed video using the event-driven data to enable deblurring. Both used in their event-driven readout a row-based scanning with an architecture to minimize loss of events and with selectable adaptation to allow the skipping over areas with no activity. Andreas Suess of Omnivision (Paper 5.1) described a three-stack 1 Mpix sensor with a top-layer with CIS pixels devices, a face-to-face layer with event-driven pixel circuits and a bottom layer with readout circuitry, achieving a small stacked die size. Kazutoshi Kodama of SONY (Paper 5.2) described a two-stack 2-Mpix sensor with the face-to-face bottom layer contain the peripheral circuitry adjacent to the event-driven circuits placed under the image array. Both when run in adaptive mode allowed event-driven rates of 4.6 Keps.

Atsumi Niwa of SONY (Paper 5.3) described achieving the record smallest event-driven pixel pitch of 2.97?m by using a single comparator per readout to sequentially capture the rising and falling intensity events. The image sensor also included circuitry to provide auto-thresholding to account for shifting contrast in the scene and to address illumination flicker.

Hyuncheol Kim of Samsung (Paper 5.4) described the design of a 2×2 pixel with 0.64?m photodiode pitch that enabled all-directional PDAF. To achieve this, a large full-well of 20ke- and a read noise of 0.98e-, the design included internal overflow within each quad of photodiodes and in the use of quarter-annulus source-follower gate.

Min Liu of the Chinese Academy of Sciences (Paper 5.5) described a silicon-based 16kpix Tera Hertz imaging array. The advantage of THz imaging is the combination of high resolution with non-destructive depth penetration. The 60?m pixel is built in a 180nm CMOS process with the antenna formed as a square of Metal 6. The on-chip circuitry incorporates filtering and chopping to reduce noise and column-based 1-bit I-ADC to provide good linearity in a small area.

Byungchoul Park of Yonsei University (Paper 5.6) described the ROIC for a Gd₂O₂S scintillator-based x-ray detector that is demonstrated for dental or machine inspection applications. The pixel is based on a silicon SPAD and incorporates a series of design features to enhance performance. The design incorporates twin ping pong counters to create a seamless digital global shutter. It includes active quenching activated by counter overflow and global reset for global shutter operation. Imagery was shown both for low-dose photon-counting mode and for a high-dose extrapolation mode that extends total counts by 400x. Radiation hardness data shows expected 8-year life for part.

Karim Ali Ahmed of National University of Singapore (Paper 5.7) presented an image sensor aimed at surveillance with features on-chip circuitry for illumination-based energy harvesting and for a combination of feature extraction and of the tile-based determination for when objects enter or leave the scene. The pixel is a 12T dynamic-least-significant-bit-circuit producing 4-bit time-based output. The goal of this combination is to operate so energy harvesting enables minimum power usage to provide extended battery operation.

Rahul Gulve of the University of Toronto (Paper 5.8) presented a VGA-format image sensor which can produce individually or simultaneously global shutter imagery and HDR flux triggered readout. The use of random access dual-tap pixel operation increases high-speed global shutter updates with no light lost. The HDR mode takes a different approach from the standard single slope readout both in using a 3T pixel to directly monitor flux and the multiple sampling of a non-linear reference waveform combined with a look-up-table-based regression to provide high speed acquisition. The image sensor allowed an external ramp and so acted as a test bed for evaluating different reference waveforms with the conclusion that the best waveform is a sine wave. The performance using 25 subexposures mapping a 5×5 tile produced a 25-frame burst-mode video at 4.7 kfps.

The session was well attended with a good number of familiar faces. The papers were well-presented with good technical quality. The one thing missing in the session was attendee participation for Q&A. This may be due to the novelty and variety of the presentations making it difficult to frame succinct questions on the spot.

The sensors from Papers 5.1, 5.2, 5.3 and 5.6 were part of the evening demonstration session. The interest and discussion around the tables seemed lively.

Dan McGrath.

Time is flying, and again another year has (almost) passedby.  A first year post-covid ?!  At least what we have seen and experienced are again in-person meetings and conferences.  My very first in-person gathering since 26 months was the Image Sensors Europe conference in London.  It was such a pleasure to see that many “old” colleagues again.  Also the Harvest Imaging Forum could take place as an in-person event (although I added the option to attend on-line as well).

So the year 2022 could be seen as the year in which we tried to move again back to the old “normal”.  But at the moment that we were looking forward to that, the world was hit by a new crisis in Ukraine with the energy crisis as a result.  First marketing reports indicate that the successive world-level threats have also their negative influence on the image sensor business.  But the same marketing people also predict a re-growth of market in the second half of 2022.  Let’s cross our fingers.

If I look back to the year 2022 in relation to Harvest Imaging, then first of all I am more than happy to share the news that 50 years ago Uncle Neil released his album, called “Harvest”. The tille of that album inspired me to use the name of “Harvest Imaging” to my own little business.  Harvest Imaging enjoyed its 15th birthday in 2022, and it is pretty sure that Harvest Imaging will never reach a 50th anniversary.  But for the moment still the same business aspects are being addressed by Harvest Imaging :

• training and teaching : most of the courses are now on-line, because (due to Covid ?) also USA and FE discovered the possibilities to get tailored trainings and courses delivered by Harvest Imaging.  In contradiction to foregoing years, the majority of training days were booked by overseas customers and no longer by EU customers.  Looking to 2023, all trends in the training business of Haarvest Imaging will continue : partly back to in-class courses, the majority still will be on-line, mainly for overseas customers,
• consulting : most of the working time in 2022 was devoted to training and teaching, not that much time was left for consulting.  I am sorry that I had to disappoint some customers when they were asking for consulting work.  One of the issues of running a service business is the fact that you can sell your hours only once,
• technical projects : in the year 2022 I finished my evaluations on angular dependency of the (parastic) light sensivitity of an existing global shutter image sensor.  The results were presented at the Image Sensors Europe conference and published in the special issue on Solid-State Image Sensors of the IEEE Transactions on Electron Devices.  The material presented and published can be found on the webpages of Harvest Imaging.  It remains a lot of fun to do all the experimental stuff myself, and still learn from it.  I can advice this to every (solid-state imaging) engineer,
• Harvest Imaging Forum : due to Covid the 2021 edition of the Forum had to be postponed to 2022.  But after a very slow start of the registrations, finally the forum could take place as a hybrid event.  The comments from the participants was very positive, so also in 2023 the Forum will be combine on-site and on-line attendance.   Information about the 2023 version of the Forum can be found on the webpages of Harvest Imaging.

Isn’t there nothing that will change in 2023 ?  For sure there is : mid May 2023 my contract at the Delft University of Technology will come to an end and I ask my manager to no longer extend the contract.  My last MSc student got his degree in November 2022, and my last PhD will finish his project in September 2023.  In this way my academic career will come to an end in 2023.  If I look back to my 22 years of part-time professorship (0.2 fte) at the Delft University of Technology, I “delivered” 16 MSc students and 13 PhD students.  Most of them are still working in the field of electronic imaging.

Close to the end of 2022, it is a pleasure for me to wish all my customers and readers a great Christmas period and a Happy and Healthy 2023.

Albert.

Another year passed by, and what a kind of year ?  No travel, no face-to-face meetings, no in-person conference or workshops, all gatherings on-line.  But nevertheless we survived, actually we had to make use of the technology we all helped to develop ourselves.  At least now I can show to my grandchildren when they follow on-line teaching what the result is of the work grand-daddy is doing.  “Every disadvantage has it own advantage”, is a famous saying in our language.

Also in 2021 Harvest Imaging delivered several public as well as in-house trainings.  Amazing was to experience that the USA discovered the trainings by the fact that now everything is delivered on-line.  I never had that many customers from overseas as in 2021.  Some classes were running till late at night to accomodate the time difference between the West Coast of the USA and Europe.  After the USA I expected that something similar would happen to potential customers in the Far East, but that did not happen (yet).  Also the training agenda for 2022 is again nicely filling up, mainly with in-house or tailored courses.  Next to the regular trainings, I also started with a series of videos, accessable through a video-on-demand tool.  Unique to this video-on-demand is a kind of follw-up in Q&A sessions.

My activities at the Delft University of Technology slowed down, my contract was adapted to 1 day/week.  At this moment still 1 PhD candidate is working on a high-speed CMOS image sensor, as well as 2 MSc student.  It is still fun to work with these young people, although also in this part of my work Covid is hampering the progress and the personal contact with the students.  Besides the academic work in Delft, I am still working on “private” technical projects as well.  The “Reproducibily, Variability and Reliability of CIS” project, started in 2017, was finished in 2021 and all reports are sent out to all customers who bought the reports.  Next I started a project on “Angular Dependency and Parasitic Light Sensitivity”.  Two papers are written (almost ready) to share the technical content of the findings.  The material is submitted to be published in a special issue on Image Sensors (IEEE-ED), scheduled in 2022.  Talking about publications : also in 2021 a booklet was finished that I wrote together with Guy Meynants about Single-Slope ADCs for Image Sensors.  In the past Guy and myself were competitors in the imaging business, these days we are colleagues : Guy at the University of Leuven, and myself at the Delft University of Technology.  Bringing these two worlds together was quite encouraging.  Working through the busy agendas of Guy and myself resulted in the aforementioned booklet.  We made an agreement to start writing another booklet about a CIS related topic, but both of us have a common issue : lack of time.

Another great publication, maybe the biggest of all I ever wrote in my entire career, was the plenary talk/paper at the ISSCC2021.  Too bad that the conference had to go on-line as well.  Nevertheless, my presentation was pre-recorded and after the ISSCC2021 the video was uploaded on YouTube.  Together with the number of views on the IEEE website, a total of over 5000 people watched the presentation.  This is considered as a quite high number for a technical talk.

In 2021 the International Image Sensor Workshop was scheduled to take place in Europe, but due to the well-known reasons, also the IISW2021 was organized as a virtual event.  Johannes and Vladimir acted as the general chairs of the workshop, Guy took on the role of Technical Progam Chair.  This EU-team did a great job in organizing a smooth workshop with over 500 registrants and about 100 presentations.  It is really very rewarding to see that the “youngsters” can take over the work in organizing and running the IISW.  Hopefully the pandemic will be gone before the next workshop, the plan is to have in 2023 IISW as an in-person event, again in Europe.  After IISW2021 also my position as president of IISS came to an end, Junichi Nakamura took over my duties.

Then there is one question left : what will 2022 bring ?  Well I think in the first place more of the same as in 2021.  The plans made a couple of years ago for a Summer School are now (definitely) buried because of Covid.  Unfortunately the Harvest Imaging Forum 2021 also had to be postponed and is now scheduled for June 2022.  It is not yet clear whether the real 2022 forum will be scheduled for December 2022 or whether the forum will definitely move to a June timeframe.  Also plans are in development to do new and more measurements on CIS at different temperatures.  “Never a dull moment in imaging !”.

Looking forward to “see” you in 2022, through the website or by means of the Harvest Imaging Newsletter.

Stay Healthy and Happy New Year,

Albert.

24/12/2021.

In 1981 my PhD project entered the last phase : design of a CCD line array, fabricate the device with the newly developed ITO gates and the newly developed polyimide isolation layer.  In the 3 years before, I researched the implementation of ITO in an existing CCD process, and the fabrication of a new CCD would be the proof of the pudding.

Being a PhD student, we had to do everything ourselves.  Starting with the lay-out of the CCD.  This was almost a daily fight to get access to the lay-out system (Applicon), because many people had to make use of the same system and only one machine was available at our university.  But finally, when the lay-out was ready, the layers of the chip had (literally) to be cut into the top part of a two-film foil (we called it “stabylene” but I do not know whether this is an official name) on a scale of 200:1.  Next the structures were manually pealed off with a tweezer.  This was a very time-consuming task and needed nerves of steel.  Because every single failure made, resulted in a new start from scratch for that particular mask lay-out.

When the masks came back from the mask shop (thanks Piet) the processing of the devices could start.  At that time we were working with silicon wafers of 2 inches.  Thanks to the crew of the clean room (Viviane, Eddy, Rita), the base processing of the CCD flow chart took only a couple of weeks.  Then I could start with the deposition, anneal, etching, contacting of the ITO layers.  Everything had to be “first time right”, time because money was very limited in a PhD project.  Believe it or not, but a full lot contained exactly 4 2”-wafers !

And then the testing (thanks Tony), also here everything was done manually.  Soldering, de-soldering, re-soldering till finally the big moment : a functional device with the new material incorporated !  A 256 pixel CCD line array with ITO gates !  What a great moment.  The device realized a much larger QE than the older technology with poly-Si gates.  If I remember well the QE was increased by a factor of 2 overall, and even a factor of 4 increase in the blue part of the spectrum.  Unfortunately the dark current of the new device was also much larger than the devices fabricated in old technology.  We were not able in reducing the radiation damage introduced during the deposition of the ITO film.  Because the temperature of any annealing step after ITO deposition needed to be kept low, the interface damage could not be repaired.  A CVD deposition technique for the ITO layer could be a better alternative because CVD does not introduce interface radiation damage.  But a CVD machine to deposit ITO was not available at those times.

All together : as far as the optical characteristics of the devices were concerned the project objectives were met, but a hard price has to be paid in the form of increased leakage current and consequently a larger noise floor.  Several years later, the ITO technology was successfully and industrially incorporated by Kodak in their CCD process.  It is not known whether Kodak could benefit from the ITO work I did, but it would surprise me if it was not, because my supervisor (Gilbert) was also working as a consultant for Kodak.  And actually I hope that Kodak indeed did learn something from my PhD project, then my work has contributed to the development of the CCD technology in general.

Albert, 08-08-2021.

What an incredible year 2020 was !  Who could have forecasted this 12 months ago ?  Normally I am on the road about 50 % of my working time.  In 2020 I returned on March 12^th from the Image Sensor conference in London and since then I have been at home, I could even sleep every night in my own bed.  In the week after March 12^th all activities, trainings, conferences and other face-to-face meetings were cancelled or postponed.  It gave me the time to update my courses.  As a nice present, the invitation came to give a plenary talk at the ISSCC2021.  That is a great honour to present at the world’s top conference in the field of solid-state circuits.  The preparation of the paper and the talk took much more time than expected, but during the second quarter of the year, time was not really an issue.

But then after the Summer the opposite of the Spring happened.  Many of the postponed trainings and courses were shifted to the Fall, of course everything on-line.  In the beginning the on-line contacts felt very strange and weird, but one gets used to it.  Although I do have admit that teaching on-line is completely different of in-class courses.  You really miss the body language, the informal contacts, the joined lunches.  The participants are also much more quite during on-line events.  Much less questions, much less discussion, too bad.  Most interesting classes are the ones with most discussions, not just for me but also for the participants.

In my “Goodbye 2019” blog I announced the possibility to start with a Summer School in 2020.  Because of the well-known issues in the world, this idea was buried.  Also the Harvest Imaging Forum 2020 had to be postponed.  Too bad, but there was no other choice.  For both events, the interaction between people is the most rewarding part of participation.  And if that cannot be guaranteed, then it is better to cancel and/or to postpone.

So now that 2020 is almost completed, the question is : “What will 2021 bring ?”.  The technical courses and trainings of Harvest Imaging will continue, that is for sure.  Several courses are already booked for the Spring 2021.  Work is going on for the agenda of the second half of 2021.  Also the work on the Reproducibility, Variability and Reliability of CIS will continue.  The first part being the reproducibility and variability will come to an end after 5 years, but the experiments in the field of reliability will continue.  New stressing experiments just have started on devices with removed coverglass and removed microlenses.  Very interesting stuff to look forward to.  Don’t think that CIS devices are invulnerable !

Wishing all my readers a Merry Christmas and a Happy New Year.  Let’s hope that the problems we all are facing these days will be over in 2021.  “See” you soon.

Albert, 22-12-2020.

Actually I do not know whether the next story exactly happened 40 years ago, but at least around that time.  As a young PhD student we were invited to act as daily coach for MSc students who were working on their thesis project.  And because my own PhD project was focusing on CCDs, also the MSc projects I had to coach had to do with CCDs.

At that time one of my colleagues, Peter Schreurs, was working on an analog CCD memory for a picture-in-picture (PiP) applications, a project sponsored by Barco.  Peter designed a CCD memory of about 100 x 80 CCD cells (I do not recall the exact dimensions anymore, but it must have been something alike).  But this analog memory could also be used as an image sensor, a kind of full-frame CCD architecture.  And together with the department Traffic Control, we proposed an MSc thesis project to build a solid-state camera (based on Peter’s CCD) for traffic monitoring (measuring width, length, speed, location on the road, … of cars that passed by the camera).

There were two groups of MSc students that worked on the project.  The first group prepared the camera hardware, the second group worked on the software.  It is remarkable to look to the names of these guys : the first group was Jan Vermeiren (still in imaging, now with Caeleste) en Wim Verhaer (I lost track of him), the second group was Jan Bosiers (in imaging till very recently, just retired from Teledyne) and Ludo Pingnet (I lost track of him).  Next to the camera hardware and software to allow the complete set-up to work as a traffic monitor, the guys also build some demo set-ups.  I still remember that a small race-track was put together with some electric cars (toys) running around the track.  The CCD camera nicely could take pictures and the micro-processor attached to it could monitor the parameters of the cars passing under the camera.  It is a pity that I do not have any pictures left taken by the CCD.  The images of 100 x 80 pixels of a full-frame CCD at the end of the ‘70s were probably not of the same quality as the ones we have today in our mobile phones 😉

A second demo and test was a real life experiment : the guys were sitting on the second floor of the building near a window.  The camera was mounted on a long wooden stick and hand held outside the window, while monitoring the parking lot.  The undersigned was driving with his car in small circles around the building and underneath the camera.  In the mean time the set-up was counting how many times my car passed.  And the set-up passed the tests !

Amazing to remember how technology was developed with very limited means, but it was a lot of fun.  Every step taken in the development of the system was revealing something new.  This piece of work even resulted in my very first publication (see Harvest Imaging website, with a photograph of the race track).

We all had a great time, thanks Jan, Wim, Jan and Ludo.

Albert, 13-10-2020.

“A 0.8V multimode vision sensor for motion and saliency detection with ping-pong PWM pixel” by the National Tsing Hua Univ., Taiwan.

Energy-efficient always-on motion detection (MD) sensors are in high demand and are widely used in machine vision applications.  To achieve real-time and continuous motion monitoring, high speed low-power temporal difference imagers with corresponding processing architectures are widely investigated.  Event-based dynamic vision sensors (DVS) have been reported to reduce the redundant data an power through the asynchronous timestamped event-address readout.  But these sensors need special data processing to collect enough events for information extraction.  Noise and dynamic effects can be issues as well.  Frame-based MD rolling shutter sensors were reported to reduce the data bandwidth and power by sub-sampling operation, global shutter MD sensors were reported using in-pixel analog memory for reference image storage.  In a frame-based MD sensor, the required analog processing circuit and two successive frames for temporal difference operation comes at a cost in power, area and speed.  In this paper a frame-based MD vision sensor is presented, featuring three operation modes :

• Image capture,
• Frame-difference with on/off event detection,
• Saliency detection.

Using a low-voltage ping-pong PWM pixel and multi-mode operation, it achieves high-speed low-power full resolution motion detection, consecutive event frame reporting, and image capture features.  Moreover, saliency detection by counting the block-level event number is also implemented for efficient optic flow extraction of the companion processing chip using simple neuromorphic circuits.

“A 1280×720 back-illuminated stacked temporal contrast event-based bision sensor with 4.86 um pixels, 1.066 GEPS readout, programmable event-rate controller and compressive data-formatting pipeline” by Prophesee and Sony.

Event-based (EB) vision sensors pixel-individually detect temporal contrast exceeding a preset relative threshold to follow the temporal evolution of relative light changes and to define sampling points for frame-free pixel-level measurement of absolute intensity.  EB sensors gain popularity in high-speed low-power machine vision applications thanks to temporal precision of recorded data, inherent suppression of temporal redundancy resulting in reduced post-processing cost, and wide intra-scene dynamic range operation.

The heart of the pixel is a logarithmic responding photodiode, and every time the pixel exceeded a certain threshold in amplitude, the pixel detects “an event”.  Events can be positive and negative.  This concept is illustrated below.

The photodiode is partially pinned and the logarithmic response is realized by means of a subthreshold MOS based logarithmic photocurrent-to-voltage converter.  The chip is making use of stacking technology with a per-pixel interconnect.  The toplayer (90 nm BI CIS) consists of the photodiode plus 2 nMOS transistors, all other pixel circuitry (50 transistors) are located on the bottom layer (40 nm CMOS).  Pixel pitch is 4.86 um with a fill factor of over 77 %.  The overall power consumption of the chip depends on the number of events that are detected, e.g. at 100 kEPS the chip consumes 32 mW, at 300 MEPS, power consumption is equal to 73 mW.

The latter paper got a lot of attention, not just because of the device performance, but also because of the remarkable cooperation between the two companies.

Albert, 23 February 2020.

“A 1/2.65inch 44Mpixel CMOS image sensor with 0.7 um pixels fabricated in advanced full-depth deep-trench isolation technology” by Samsung.  Basically the title says it all.

Remarkable technology that is used to create the deep-trenches in a pixel of 0.7 um.  On the backside of envelope I calculated the trench should be around 85 nm in width, with an aspect ratio of 69.  Next an isolation is provided on the sides of the trenches and the poly-Si filling takes place.  For the latter it is even more challenging : the aspect ratio is increased to 110.  It is really incredible that these things are possible in CMOS technology.

Some numbers :

• Pixel size : 0.7 um,
• Full well : 6000 electrons,
• Temporal noise : 1.4 electron,
• Dark current at 60 deg.C : 1.3 electron.

It is not just the trenches that are further optimized in the technology (compared to the 0.8 um pixel pitch that is most probably used in the 108 Mpixel device), also the boxing of the CFA is changed : a low refractive index grid is used instead of tungsten.  This results in an increase of about 15 % In QE(green).

The sensor presented is making use of the quad Bayer structure.  This is a very attractive architecture for binning options.  With binning the SNR can be increase considerably for applications in harsh light conditions (at the expense of resolution of course).  The results are shown in the figure below.

Artilux presented “An up-to-1400 nm 500MHz Demodulated time-of-flight image sensor on a Ge-on-Si platform”.  It is of course well known that the silicon response is limited up to a wavelength of 1100 nm.  If one is interested in detection of longer wavelengths, another material than silicon is needed, for instance germanium (Ge).

The reason to go for longer wavelengths, such as in time-of-flight applications, can be found in :

• issues with eye-safety between 800 nm and 1100 nm,
• background sunlight : the sun does not emit at 1300 nm.

If one compares the absorption spectrum of germanium with the one of silicon, indeed germanium seems to be a viable candidate to replace silicon for longer wavelengths.  The paper presented puts a very thin Ge toplayer on a silicon readout circuit.  The idea is not really new, this was already done earlier by Noble Peak (USA).  A cross section of the Si readout structure provided with a thin Ge layer (using a Si carrier ?) is shown below.

The authors claim to reach a QE equal to 50 % at 1500 nm and further optimization is still possible in optimizing the microlenses for this wavelength.  Nevertheless, there still some work needed to lower the dark current.   In the ToF application a modulation depth of 90 % can be obtained at 500 MHz modulation frequency, resulting in a measurement error less than 0.5 % for a distance of 1 m.

Albert, 20 February 2020.

ISSCC 2020 (1)

A few words about the imaging papers at the International Solid-State Circuits Conference 2020.  Let’s get started with an easy one.

Sony presented a paper “A 132 dB single exposure dynamic range CMOS image sensor with high temperature tolerance”.  This paper is an extension of the one presented at IEDM 2018.  This pixel of IEDM 2018 is composed out of two photodiodes (small one for highlights, big one for lowlights).  At the IEDM 2018 version, they were making use of three different sensitivity levels to create the high dynamic range.  In the ISSCC2020 version, an extra sensitivity level is added to create a high dynamic range by means of four different sensitivity levels.  So in total two photodiodes, the large one has two conversion gains, the small one has a single conversion gain, with the capability of overflow to an in-pixel capacitor.  To operate the device in low noise, 8 readout cycles per pixel are needed, because for every signal (low/high conversion gain, small/large photodiode) also a reference signal readout is needed.  The area ratio between the two photodiodes is reported to be 14.5, in the 2018 version, this ratio was 10.

The pixel structure is shown in the following figure (FC is the newly added capacitor) :

Some numbers :

• Pixel pitch : 3.0 um,
• FE 90 nm, BE 65 nm (1P4Cu), logic part :40 nm (1P6CU,1AL),
• Highest full well : 165,800 electrons, (this high full well is reached thanks to a vertical transfer gate instead of the classical planar one).
• Random noise 0.6 electrons,
• Single exposure (multiple reads) dynamic range : 132 dB.

The device is fabricated in a stacked technology, connection between the top and bottom layer is done on column level (TSV ?)

The title also refers to a high temperature tolerance, but in the presentation nothing was mentioned what has being done to obtain this high temperature tolerance, neither what was the gain in temperature tolerance w.r.t. other devices.

A global shutter paper was presented by Samsung : “A 2.1 e temporal noise and -105 dB parasitic light sensitivity backside-illuminated 2.3 um pixel voltage domain global shutter CMOS image sensor using high-capacity DRAM capacitor technology”.  These days the titles of these talks are so long that actually all ingredients of the talk are already included in the title.

The paper is concentrating on the voltage domain global shutter option with correlated double sampling in the pixel.  The authors referred to the issues with parasitic light sensitivity of the storage node in a charge domain global shutter and to the issues with kTC noise in the voltage domain global shutters if the storage capacitors are too small.  The latter is solved in this paper by incorporating a high-capacity DRAM storage capacitor on top of the pixel.  Because the technology is BSI, “plenty” of room is available to build an extra capacitor at the front-side of the pixel.  This capacitor is not a stacked one, it is realized during the CMOS fabrication on top of pixel, in the third dimension.

The pixel itself has a classical structure that is known for voltage domain global shutter pixels, but a few extras are added : an extra transistor between the floating diffusion and the reset transistor to create a dual conversion gain, a clamping transistor to perform in-pixel CDS (based on clamping) and an extra capacitor that allows to short-circuit the in-pixel CDS and storage node, and actually allows the pixel to operate in the rolling shutter mode.

The device realizes the following performance :

• Pixel size 2.3 um,
• Stacked BSI (but the DRAM capacitor is not stacked !)
• Saturation level 12000 e^– at low gain
• PLS : -115 dB (green)
• Performance at 940 nm : PLS = -95 dB, QE = 42 %,
• Read noise : 2.1 e^– for 18 dB of gain,
• Frame rate : 120 fps.

The heart of this pixel is of course the DRAM capacitor on top of the front side of the pixel, a cross section is shown below :

(more to follow)

Albert, 19 February 2020.