In the previous blog, the measurement of the full well capacity (FWC) was explained based on the measurement of the output signal versus the input signal. The input signal was generated by a constant light source in combination with a varying exposure time. But once all output data is available, not only the average value of the pixels can be calculated but also the temporal noise level for every pixel. This will be done in this blog.
From the discussion of the photon-transfer curve and its properties, it was learned that when the photon shot noise is the dominant noise source, the following formula can be written down :
ntemp2 = k×(Sout – Soff)
with :
ntemp : the total temporal noise on pixel level,
k : conversion gain,
Sout : the average signal on pixel level,
Soff : offset value, or the average signal for 0 s exposure time.
(Normally I use a sigma-symbol for the noise, but the bloody software does not accept the sigma-symbol.)
So instead of looking after the saturation level of the signal, one can also look after the saturation or the peak level in noise and try to calculate the FWC based on the noise measurements. The FWC is defined at the point at which the temporal noise reaches its maximum value.
1) Saturation of the sensor is larger than maximum value of the ADC.
In such a case, most of the time the maximum value of the sensor or camera ADC is set such that the complete ADC range covers the linear part of the sensor’s output response. An example of a camera in which the ADC defines the maximum output level of the system is shown in Figure 1, where the sensor noise variance is shown as a function of the exposure time (the data already collected in the previous blog is reused here).
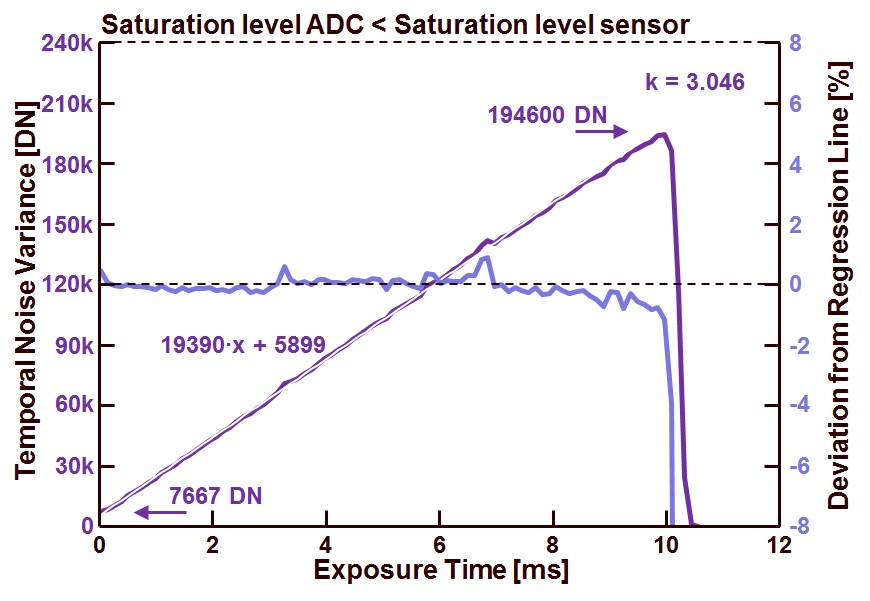
Figure 1 : Noise variance as a function of exposure time, under a constant illumination level.
Shown is the temporal noise variance as a function of the exposure time at a constant illumination level (the exact value of the light input is not important for this measurement, as long as it stays constant). As can be observed, the transition from a monotonically increasing output value of the variance to zero goes pretty abruptly. This is a clear indication that the ADC defines the saturation level. Moreover, the peak value of the temporal noise variance is equal to 194,600 DN.
For this example, the definition of the full well capacity is equal to the variance peak value divided by k, minus the offset value of the noise variance at 0 s exposure time divided by k, or (194,600/k) – (7667/k) = 63,887 – 2517 = 61,370 DN.
Taking into account the conversion gain of the sensor (3.046 DN/electron, for the TIFF format it is 64x larger than what can be measured at the output of the sensor), this results in a FWC = 20,148 electrons.
2) Saturation of the sensor is smaller than maximum value of the ADC.
In this case, the FWC needs a clear definition : is FWC referring to the saturation level of the sensor/camera, or is FWC referring to the maximum linear part of the sensor’s output swing ? The former can be referred to a FWCsat, while the latter can be indicated by FWClin. But now the question arises : how to define the linear part of the sensor’s output swing ? In the previous blog, FWClin was set at the point where the sensor’s output deviated maximum 3 % of the linear behavior. Taking that definition and transferring it to the noise variance measurement, now FWClin will be defined at the point where the noise variance deviates maximum k×(3 %) = 4.5 %.
An example of a camera in which the ADC maximum output value is larger than the saturation level of the sensor is shown in Figure 2.

Figure 2 : Noise variance as a function of exposure time, under a constant illumination level.
Shown is the temporal noise variance as a function of the exposure time with a constant illumination level (the exact value of the light input is not important for this measurement, as long as it stays constant). As can be observed, the transition from a monotonically increasing output value to a decrease of the noise variance goes smoothly. This is a clear indication that the ADC is NOT defining the saturation level of the system.
For this example, the definition of the full well capacity at saturation is equal to the maximum level of the noise variance divided by k, minus the offset of the noise variance measured at 0 s exposure time and also divided by k, or (41,260/k) – (2389/k) = 27,013 DN. Taking into account the conversion gain of the sensor (1.493 DN/electron), this results in a FWCsat = 18,093 electrons.
But as mentioned before, this is only half of the story, because the sensor’s response is very nonlinear close to saturation. For that reason the linearity (INL) of the sensor is characterized and plotted in Figure 2 as well. At the point where the real output characteristic deviates 4.5 % from its regression line, the FWClin is defined. In this example, the following number can be found : (39,780/k) – (2389/k) = 25,044 DN, translating in FWClin = 16,774 electrons.
It should be clear that this last number is very much depending on the definition of FWClin. If the 4.5 % deviation is translated in 1.5 %, the value for the FWClin will become smaller, or if the 4.5 % deviation is translated in 7.5 %, the opposite becomes valid.
Note : the data shown in Figures 1 and 2 are obtained from the same sensor, with the same light input. The difference between the two measurements is a difference in camera setting, such that the analog gain of the sensor and the reference voltage of the ADC result in an overall camera gain difference of a factor of 2.
Explained in this blog is the measurement of FWC based on noise variance. Again it can be learned that the values obtained for the FWC strongly depend on the exact definition of the full well capacity. Lesson to take away : if the FWC is specified in an image sensor’s datasheet, first ask yourself “How is the FWC defined ?”.
See you next time !
Albert, 04-11-2013.

