Over the last couple of months, Harvest Imaging performed measurements on the PDAF pixels present in an existing, commercially available camera. The results of these measurements, including explanations for the PDAF performance/behaviour are written down in an extensive report. This report is now available. Unfortunately not free of charge, because quite some resources were invested in developing hard- and software tools to extract the right data directly out of the sensor. If you are interested in the report, please drop me a mail (info “at” harvestimaging “dot” com), and I am happy to send you a quotation to get a copy of the report.
Find below the table of contents of the report, as well as a list of figures included in the report.
Kind regards, Albert.
Table of Contents
List of Figures
Introduction
Working principle of PDAF pixels
Theoretical implementation of PDAF pixels
Practical implementation of PDAF pixels
From the theory to the reality
Measurement 1 : influence of F-number
Measurement 2 : influence of the object distance
Measurement 3 : influence of the object angle
Measurement 4 : influence of the PDAF location on the sensor
Measurement 5 : influence of the object colour
Conclusions
Acknowledgement
References
List of Figures
Figure 1. Imaging with a positive lens
Figure 2. Requirement to have an image in-focus at the surface of the image sensor
Figure 3. illustration of rear focus, in-focus and front focus
Figure 4. Illustration of two different rear focus situations
Figure 5. Illustration of two different front focus situations
Figure 6. Optical ray formation from the object till the photodiode of an image sensor
Figure 7. Optical ray formation from the object till the partly optically-shielded photodiodes/pixels of an image sensor
Figure 8. Aptina’s MT9J007C1HS architecture with 9 rows containing auto-focus pixels based on phase detection
Figure 9. Microphotograph of one of the AF rows
Figure 10. Magnified view of an AF row
Figure 11. Microphotograph of an AF row
Figure 12. Sensor architecture indicating the various AF lines as well as the different zones used to read the sensor
Figure 13. Image taken from a random scenery with the AF option switched ON
Figure 14. Analysis of the signals of AF-line 5 in zone 5
Figure 15. Image taken from the same scenery as in Figure 13 with the AF option switched OFF and manually focused on the “macro” position
Figure 16. Analysis of the signal of AF-line 5 in zone 5 in the case the AF system is forced to “macro” position
Figure 17. Image taken from the same scenery as in Figure 13 with the AF option switched OFF, and manually focused on the “infinity” position
Figure 18. Analysis of the signals of AF-line 5 in zone 5 in the case the AF system is forced to “infinity” position
Figure 19. Odd and even PDAF signal for an object place 50 cm in front of the camera and the lens switched to auto-focus “ON”
Figure 20. Odd and even PDAF signal for an object placed 50 cm in front of the camera and the lens focusing on “infinity”
Figure 21. Odd and even PDAF signal for an object place 50 cm in front of the camera and the lens focusing on “macro”
Figure 22. Depth-of-field as a function of the object distance for 3 F-numbers, the dotted lines indicate the corresponding hyper-focal distances
Figure 23 PDAF pixel shift as a function of F-number for an object 50 cm in front of the camera and auto focusing
Figure 24 PDAF pixel shift as a function of F-number for an object 50 cm in front of the camera and focusing at “infinity”
Figure 25 PDAF pixel shift as a function of F-number for an object 50 cm in front of the camera and focusing at “macro”
Figure 26 Front-focus situation
Figure 27. PDAF pixel shift as a function of object distance and auto-focus setting of the camera, with F2.8
Figure 28. PDAF pixel shift as a function of object distance and auto-focus setting of the camera, with F5.6
Figure 29. PDAF pixel shift as a function of object distance and auto-focus setting of the camera, with F11
Figure 30. PDAF pixel shift as a function of object distance, lens auto-focus setting on “infinity” and with F2.8
Figure 31. PDAF pixel shift as a function of object distance, lens auto-focus setting on “infinity” and with F5.6
Figure 32. PDAF pixel shift as a function of object distance, lens auto-focus setting on “infinity” and with F11
Figure 33. PDAF pixel shift as a function of object distance, lens auto-focus setting on “macro” and with F2.8
Figure 34. PDAF pixel shift as a function of object distance, lens auto-focus setting on “macro” and with F5.6
Figure 35. PDAF pixel shift as a function of object distance, lens auto-focus setting on “macro” and with F11
Figure 36. PDAF pixel shift as a function of object distance, lens focusing fixed at 60 cm and F2.8
Figure 37. PDAF pixel shift as a function of object distance, lens focusing fixed at 60 cm and F5.6
Figure 38. PDAF pixel shift as a function of object distance, lens focusing fixed at 60 cm and F11
Figure 39. PDAF pixel shift as a function of object angle and auto-focus setting of the camera, with F2.8
Figure 40. PDAF pixel shift as a function of object angle and auto-focus setting of the camera, with F11
Figure 41. PDAF pixel shift as a function of object angle, lens focusing on “infinity” and with F2.8
Figure 42. PDAF pixel shift as a function of object angle, lens focusing on “infinity” and with F11
Figure 43. PDAF pixel shift as a function of object angle, lens focusing on “macro” and with F2.8
Figure 44. PDAF pixel shift as a function of object angle, lens focusing on “macro” and with F11
Figure 45. PDAF pixel shift as a function of the PDAF location in readout zone 5 and auto-focus setting of the camera, with F2.8
Figure 46. PDAF pixel shift as a function of the PDAF location in readout zone 5 and auto-focus setting of the camera, with F11
Figure 47. PDAF pixel shift as a function of the PDAF location in readout zone 5 and lens focusing on “infinity” and with F2.8
Figure 48. PDAF pixel shift as a function of the PDAF location in readout zone 5 and lens focusing on “infinity” and with F11
Figure 49. PDAF pixel shift as a function of the PDAF location in readout zone 5 and lens focusing on “macro” and with F2.8
Figure 50. PDAF pixel shift as a function of the PDAF location in readout zone 5 and lens focusing on “macro” and with F11
Figure 51. Location of the various PDAF regions under test
Figure 52. PDAF pixel shift as a function of the PDAF location on AF-line 5 and on the diagonal with auto-focus setting of the camera and F2.8
Figure 53. PDAF pixel shift as a function of the PDAF location on AF-line 5 and on the diagonal with auto-focus setting of the camera and F11
Figure 54. PDAF pixel shift as a function of the PDAF location on AF-line 5 and on the diagonal with focus set to “infinity” and F2.8
Figure 55. PDAF pixel shift as a function of the PDAF location on AF-line 5 and on the diagonal with focus set to “infinity” and F11
Figure 56. PDAF pixel shift as a function of the PDAF location on AF-line 5 and on the diagonal with focus set to “macro” and F2.8
Figure 57. PDAF pixel shift as a function of the PDAF location on AF-line 5 and on the diagonal with focus set to “macro” and F11
Figure 58. Pulses used to measure the PDAF pulse shifts in zones 2 to 5 on the AF-line 5, lens focus at “infinity” and F2.8
Figure 59. Incoming rays for a PDAF pair at the edge of the sensor
Figure 60. Pulses used to measure the PDAF pulse shifts in zones 2 to 5 on the AF-line 5, lens focus at “macro” and F11
Figure 61. Odd and even pulses in AF-line 5, in AF-line 5 + 1 line and in AF-line 5 + 2 lines, with green light input, F2.8 and focusing at “infinity”
Figure 62. Odd and even pulses in AF-line 5, in AF-line 5 + 1 line and in AF-line 5 + 2 lines, with green light input, F2.8 and focusing at “infinity”
Figure 63. Odd and even pulses in AF-line 5, in AF-line 5 + 1 line and in AF-line 5 + 2 lines, with green light input, F2.8 and focusing at “infinity”
Figure 64. PDAF pixel shift as a function of object colour and auto-focus setting of the camera, with F2.8
Figure 65. PDAF pixel shift as a function of object colour and auto-focus setting of the camera, with F11
Figure 66. PDAF pixel shift as a function of object colour, lens focusing on “infinity” and with F2.8
Figure 67. PDAF pixel shift as a function of object colour, lens focusing on “infinity” and with F11
Figure 68. PDAF pixel shift as a function of object colour, lens focusing on “macro” and with F2.8
Figure 69. PDAF pixel shift as a function of object colour, lens focusing on “macro” and with F11

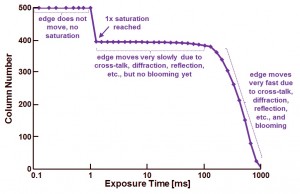
![// Captured 10:10:01 - Tuesday, August 25, 2015//// Frame 1 of 10 frames// Sensor info:// Width = 752// Height = 480// Image Format = Bayer 10// Subformat = BGGR// Sensor output = 10 bits per pixel//// .TIF file (RGB 48Bpp)//// Application version info:// Application name = DevWare.exe// Application version = 3.1.0.21// Application type = 3.1-Beta8// Application date = 12/04/2009// Firmware version = D.28//// Camera info:// productID = 0x100D Version = 0xC1// productName = Aptina Imaging DEMO2X// transportName = USB 2.0// num_chips = 1// sensor->sensorName = MI-0351// sensor->versionName = REV4// sensor->sensorFileName = sensor_dataMT9V024-REV4.sdat//// Sensor Fuse info:// FuseID: 308F9B95DFB5246B// Revision: 4// Silicon Option: --// // Windows OS info:// Display resolution = 1440x900 at 32bpp// OS Versioninfo = (5, 1, 2600, 2, Service Pack 2, 2, 0)// Microsoft Windows XP // Service Pack 2//// Processor info:// 1828 MHz// GenuineIntel// Intel(R) Core(TM)2 CPU T5600 @ 1.83GHz// 38 percent of memory is in use.// Memory 1014 MB (total)// Memory 625 MB (available)// Intel Pentium III//// USB 2.0 Enhanced Host Controllers:// Service: usbehci// Driver File: C:WINDOWSsystem32DRIVERSusbehci.sys// File Version: 5.1.2600.2180// Device Desc: Standard Enhanced PCI to USB Host Controller//// Aptina Imaging Camera Driver Info:// Service: MIUSB2// Driver File: C:WINDOWSSystem32Driversmiusb2.sys// File Version: 5.1.0.3508// Found Device: Vid_0634&Pid_100d// Service CYUSB not found// Service CYUSB not found[ColorPipe State]STATE= Display Zoom, 13STATE= Display Zoom Percent, 100STATE= Master Clock, 13500897STATE= Update Sensor FPS, 0STATE= Allow Update Sensor FPS, 1STATE= BitDepth, 10STATE= Filter, 3STATE= X Offset, 0STATE= Y Offset, 1STATE= Auto Offset, 1STATE= CFA Pattern, 0STATE= RGBC BiWindow, 2STATE= Monochrome, 1STATE= True Black Enable, 0STATE= True Black Level, 42STATE= Auto Luma Range, 1STATE= Luma Lo, 0STATE= Luma Hi, 255STATE= Unswizzle Mode, 3STATE= Swap 12-bit LSBs, 0STATE= Deinterlace Mode, 3STATE= Output Channel, 0STATE= Output BwColor, 0STATE= sRGB Color Standard, 0STATE= Color Correction, 0STATE= Gamma, 9STATE= Black Correct, 5STATE= Saturation, 10STATE= Contrast, 25STATE= Aperture Enable, 0STATE= Aperture, 5STATE= Black CCM Kill Enable, 0STATE= Black CCM Kill A, 240STATE= Black CCM Kill B, 160STATE= Black CCM Kill C, 80STATE= Green Balance Enable, 0STATE= Green Balance Apos, 128STATE= Green Balance Bpos, 10STATE= Green Balance Aneg, -128STATE= Green Balance Bneg, 10STATE= Auto Exposure, 0STATE= Auto Exposure Target, 50STATE= Auto Exposure Stability, 6STATE= Auto Exposure Speed, 30STATE= Auto Exposure Minimum FPS, 5STATE= Auto Exposure Flicker Filter, 0STATE= Auto Exposure Soft Limit, 33STATE= Auto Exposure Soft Gain Limit, 40STATE= Auto Exposure Software Gain Limit, 100STATE= Auto Exposure Freeze Gains, 0STATE= Auto Exposure Fade Saturation, 1STATE= Auto Exposure Fade Aperture, 1STATE= Auto Exposure Fade Target, 1STATE= Auto Exposure Inner Zone, 50STATE= Auto Exposure Outer Zone, 50STATE= Software Gain, 1000STATE= Mechanical Shutter Same, 1STATE= Mechanical Shutter Time, 33333STATE= Mechanical Shutter Delay, 0STATE= White Balance, 3STATE= WB Speed, 15STATE= WB Adjust Gains, 0STATE= WB Manual Position, 40STATE= WB Manual RedGreen, 100STATE= WB Manual BlueGreen, 100STATE= WB Interpolate Saturation, 1STATE= WB Normalize Matrix, 1STATE= AWB Weight Map Method, 0STATE= AWB Weight Map X Scale, 0STATE= AWB Weight Map Y Scale, 0STATE= AWB Weight Map X Shift, 0STATE= AWB Weight Map Y Shift, 0STATE= AWB Weight Map X Center, 0STATE= AWB Weight Map Y Center, 0STATE= AWB Weight Map Angle Sin, 0STATE= AWB Weight Map Angle Cos, 0STATE= AWB Weight Map Luma Low, 0STATE= AWB Weight Map Luma High, 0STATE= Minimum Gain, 1000STATE= Show Min Gain As 1, 1STATE= Default Relative Red Gain, 1000STATE= Default Relative Blue Gain, 1000STATE= Relative Red Gain, 1000STATE= Relative Blue Gain, 1000STATE= Lens Correction Enable, 0STATE= Lens Correction Falloff, 100STATE= Lens Correction Overlay, 0STATE= Lens Correction Center X, 376STATE= Lens Correction Center Y, 240STATE= Lens Correction Coeff Prec, 16STATE= Lens Correction Wide Angle, 0STATE= Lens Center Red X, 376STATE= Lens Center Red Y, 240STATE= Lens Center Green1 X, 376STATE= Lens Center Green1 Y, 240STATE= Lens Center Green2 X, 376STATE= Lens Center Green2 Y, 240STATE= Lens Center Blue X, 376STATE= Lens Center Blue Y, 240STATE= Lens Center Overlay, 0STATE= Lens Sim Sensor, 0STATE= Lens Sim Sensor Rev, 0STATE= Lens Sim Enable Pwq, 0STATE= Lens Sim Enable Poly, 0STATE= Noise Removal, 0STATE= Noise Removal Level, 25STATE= Noise Removal K1, 2000STATE= Noise Removal K2, 1800STATE= Noise Removal K3, 1000STATE= Noise Removal Edges, 1STATE= Noise Removal Kernel, 0STATE= HiDy 14bits, 0STATE= HiDy NR Enable, 0STATE= HiDy PreWB Autogain, 1STATE= HiDy TM Apply S-Curve, 1STATE= HiDy TM Enable LTM, 1STATE= Defect Enable, 0STATE= Defect Max, 1000STATE= Defect Auto Defect Correction, 0STATE= Flash Lamp, 0STATE= Still Global Reset, 0STATE= Global Reset Bulb, 0STATE= Num Capture Frames, 10STATE= Still Mode, 1STATE= Still Capture Average, 0STATE= Still Capture Timeout, 5STATE= Delay before snap, 0STATE= Save 24bpp BMP, 0STATE= Save RAW, 0STATE= Save TXT, 0STATE= Save HEX, 0STATE= Save ITX, 0STATE= Save RAW TIFF, 0STATE= Save 48bpp COLOR TIFF, 1STATE= Save JPEG, 0STATE= Save RAW JPEG, 0STATE= Save BMP Info, 0STATE= JPEG Quality (1-100), 100STATE= Save RAW PNG, 0STATE= Save PNG, 0STATE= Save DNG, 0STATE= Save Selection Rectangle, 0STATE= ICC Profile, 0STATE= Video Screen Capture, 1STATE= RAM Capture, 0STATE= RAM Capture MB, 512STATE= RAM Capture Cycle, 1STATE= WB Xenon Red Gain, 1024STATE= WB Xenon Blue Gain, 1024STATE= WB Led Red Gain, 1024STATE= WB Led Blue Gain, 1024STATE= MAE Overlay, 0STATE= Noise Image Type, 0STATE= Noise Frames, 50STATE= Strip FSP, 1STATE= Thumbnail Overlay, 1STATE= Check Thumbnail Table, 0STATE= CRA Overlay, 0STATE= Allow FAR Access, 1STATE= Pure Raw, 0STATE= AWB Incandescent, 1.3 -0.11 -0.18 -0.47 2.03 -0.49 -0.86 -0.79 5.66STATE= AWB Sun, 2.13 -0.09 -0.15 -0.44 2.09 -0.5 -0.1 -0.31 1.97STATE= AWB Incandescent Gain, 1 1STATE= AWB Sun Gain, 1 1STATE= WB Custom, 1 0 0 0 1 0 0 0 1STATE= WB Custom Xenon, 1 0 0 0 1 0 0 0 1STATE= WB Custom Led, 1 0 0 0 1 0 0 0 1STATE= AWB Weight Map, 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0STATE= Lens Curve Red, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= Lens Curve Green1, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= Lens Curve Green2, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= Lens Curve Blue, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= RGBC Sigma_S, 1STATE= RGBC Sigma_I, 0.005STATE= RGBC Smooth_Th, 0.1STATE= HiDy Matrix, 1.6475 -0.7464 0.0989 -0.0636 1.0086 0.055 -0.0266 -0.8366 1.8632STATE= HiDy NR Noise Model Coef, 1STATE= HiDy PreWB Gb, 1STATE= HiDy PreWB Gr, 1STATE= HiDy TM Peak Percent, 0.003STATE= HiDy TM Sharp S, 2STATE= Gain Table, (null)](http://harvestimaging.com/blog/wp-content/uploads/2015/08/next_blog_11-300x191.jpg)
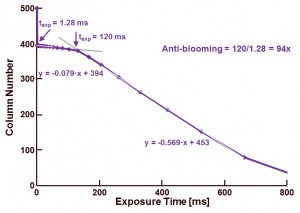
![// Captured 10:11:22 - Tuesday, August 25, 2015//// Frame 1 of 10 frames// Sensor info:// Width = 752// Height = 480// Image Format = Bayer 10// Subformat = BGGR// Sensor output = 10 bits per pixel//// .TIF file (RGB 48Bpp)//// Application version info:// Application name = DevWare.exe// Application version = 3.1.0.21// Application type = 3.1-Beta8// Application date = 12/04/2009// Firmware version = D.28//// Camera info:// productID = 0x100D Version = 0xC1// productName = Aptina Imaging DEMO2X// transportName = USB 2.0// num_chips = 1// sensor->sensorName = MI-0351// sensor->versionName = REV4// sensor->sensorFileName = sensor_dataMT9V024-REV4.sdat//// Sensor Fuse info:// FuseID: 308F9B95DFB5246B// Revision: 4// Silicon Option: --// // Windows OS info:// Display resolution = 1440x900 at 32bpp// OS Versioninfo = (5, 1, 2600, 2, Service Pack 2, 2, 0)// Microsoft Windows XP // Service Pack 2//// Processor info:// 1828 MHz// GenuineIntel// Intel(R) Core(TM)2 CPU T5600 @ 1.83GHz// 38 percent of memory is in use.// Memory 1014 MB (total)// Memory 619 MB (available)// Intel Pentium III//// USB 2.0 Enhanced Host Controllers:// Service: usbehci// Driver File: C:WINDOWSsystem32DRIVERSusbehci.sys// File Version: 5.1.2600.2180// Device Desc: Standard Enhanced PCI to USB Host Controller//// Aptina Imaging Camera Driver Info:// Service: MIUSB2// Driver File: C:WINDOWSSystem32Driversmiusb2.sys// File Version: 5.1.0.3508// Found Device: Vid_0634&Pid_100d// Service CYUSB not found// Service CYUSB not found[ColorPipe State]STATE= Display Zoom, 13STATE= Display Zoom Percent, 100STATE= Master Clock, 13500897STATE= Update Sensor FPS, 0STATE= Allow Update Sensor FPS, 1STATE= BitDepth, 10STATE= Filter, 3STATE= X Offset, 0STATE= Y Offset, 1STATE= Auto Offset, 1STATE= CFA Pattern, 0STATE= RGBC BiWindow, 2STATE= Monochrome, 1STATE= True Black Enable, 0STATE= True Black Level, 42STATE= Auto Luma Range, 1STATE= Luma Lo, 0STATE= Luma Hi, 255STATE= Unswizzle Mode, 3STATE= Swap 12-bit LSBs, 0STATE= Deinterlace Mode, 3STATE= Output Channel, 0STATE= Output BwColor, 0STATE= sRGB Color Standard, 0STATE= Color Correction, 0STATE= Gamma, 9STATE= Black Correct, 5STATE= Saturation, 10STATE= Contrast, 25STATE= Aperture Enable, 0STATE= Aperture, 5STATE= Black CCM Kill Enable, 0STATE= Black CCM Kill A, 240STATE= Black CCM Kill B, 160STATE= Black CCM Kill C, 80STATE= Green Balance Enable, 0STATE= Green Balance Apos, 128STATE= Green Balance Bpos, 10STATE= Green Balance Aneg, -128STATE= Green Balance Bneg, 10STATE= Auto Exposure, 0STATE= Auto Exposure Target, 50STATE= Auto Exposure Stability, 6STATE= Auto Exposure Speed, 30STATE= Auto Exposure Minimum FPS, 5STATE= Auto Exposure Flicker Filter, 0STATE= Auto Exposure Soft Limit, 33STATE= Auto Exposure Soft Gain Limit, 40STATE= Auto Exposure Software Gain Limit, 100STATE= Auto Exposure Freeze Gains, 0STATE= Auto Exposure Fade Saturation, 1STATE= Auto Exposure Fade Aperture, 1STATE= Auto Exposure Fade Target, 1STATE= Auto Exposure Inner Zone, 50STATE= Auto Exposure Outer Zone, 50STATE= Software Gain, 1000STATE= Mechanical Shutter Same, 1STATE= Mechanical Shutter Time, 33333STATE= Mechanical Shutter Delay, 0STATE= White Balance, 3STATE= WB Speed, 15STATE= WB Adjust Gains, 0STATE= WB Manual Position, 40STATE= WB Manual RedGreen, 100STATE= WB Manual BlueGreen, 100STATE= WB Interpolate Saturation, 1STATE= WB Normalize Matrix, 1STATE= AWB Weight Map Method, 0STATE= AWB Weight Map X Scale, 0STATE= AWB Weight Map Y Scale, 0STATE= AWB Weight Map X Shift, 0STATE= AWB Weight Map Y Shift, 0STATE= AWB Weight Map X Center, 0STATE= AWB Weight Map Y Center, 0STATE= AWB Weight Map Angle Sin, 0STATE= AWB Weight Map Angle Cos, 0STATE= AWB Weight Map Luma Low, 0STATE= AWB Weight Map Luma High, 0STATE= Minimum Gain, 1000STATE= Show Min Gain As 1, 1STATE= Default Relative Red Gain, 1000STATE= Default Relative Blue Gain, 1000STATE= Relative Red Gain, 1000STATE= Relative Blue Gain, 1000STATE= Lens Correction Enable, 0STATE= Lens Correction Falloff, 100STATE= Lens Correction Overlay, 0STATE= Lens Correction Center X, 376STATE= Lens Correction Center Y, 240STATE= Lens Correction Coeff Prec, 16STATE= Lens Correction Wide Angle, 0STATE= Lens Center Red X, 376STATE= Lens Center Red Y, 240STATE= Lens Center Green1 X, 376STATE= Lens Center Green1 Y, 240STATE= Lens Center Green2 X, 376STATE= Lens Center Green2 Y, 240STATE= Lens Center Blue X, 376STATE= Lens Center Blue Y, 240STATE= Lens Center Overlay, 0STATE= Lens Sim Sensor, 0STATE= Lens Sim Sensor Rev, 0STATE= Lens Sim Enable Pwq, 0STATE= Lens Sim Enable Poly, 0STATE= Noise Removal, 0STATE= Noise Removal Level, 25STATE= Noise Removal K1, 2000STATE= Noise Removal K2, 1800STATE= Noise Removal K3, 1000STATE= Noise Removal Edges, 1STATE= Noise Removal Kernel, 0STATE= HiDy 14bits, 0STATE= HiDy NR Enable, 0STATE= HiDy PreWB Autogain, 1STATE= HiDy TM Apply S-Curve, 1STATE= HiDy TM Enable LTM, 1STATE= Defect Enable, 0STATE= Defect Max, 1000STATE= Defect Auto Defect Correction, 0STATE= Flash Lamp, 0STATE= Still Global Reset, 0STATE= Global Reset Bulb, 0STATE= Num Capture Frames, 10STATE= Still Mode, 1STATE= Still Capture Average, 0STATE= Still Capture Timeout, 5STATE= Delay before snap, 0STATE= Save 24bpp BMP, 0STATE= Save RAW, 0STATE= Save TXT, 0STATE= Save HEX, 0STATE= Save ITX, 0STATE= Save RAW TIFF, 0STATE= Save 48bpp COLOR TIFF, 1STATE= Save JPEG, 0STATE= Save RAW JPEG, 0STATE= Save BMP Info, 0STATE= JPEG Quality (1-100), 100STATE= Save RAW PNG, 0STATE= Save PNG, 0STATE= Save DNG, 0STATE= Save Selection Rectangle, 0STATE= ICC Profile, 0STATE= Video Screen Capture, 1STATE= RAM Capture, 0STATE= RAM Capture MB, 512STATE= RAM Capture Cycle, 1STATE= WB Xenon Red Gain, 1024STATE= WB Xenon Blue Gain, 1024STATE= WB Led Red Gain, 1024STATE= WB Led Blue Gain, 1024STATE= MAE Overlay, 0STATE= Noise Image Type, 0STATE= Noise Frames, 50STATE= Strip FSP, 1STATE= Thumbnail Overlay, 1STATE= Check Thumbnail Table, 0STATE= CRA Overlay, 0STATE= Allow FAR Access, 1STATE= Pure Raw, 0STATE= AWB Incandescent, 1.3 -0.11 -0.18 -0.47 2.03 -0.49 -0.86 -0.79 5.66STATE= AWB Sun, 2.13 -0.09 -0.15 -0.44 2.09 -0.5 -0.1 -0.31 1.97STATE= AWB Incandescent Gain, 1 1STATE= AWB Sun Gain, 1 1STATE= WB Custom, 1 0 0 0 1 0 0 0 1STATE= WB Custom Xenon, 1 0 0 0 1 0 0 0 1STATE= WB Custom Led, 1 0 0 0 1 0 0 0 1STATE= AWB Weight Map, 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0STATE= Lens Curve Red, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= Lens Curve Green1, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= Lens Curve Green2, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= Lens Curve Blue, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= RGBC Sigma_S, 1STATE= RGBC Sigma_I, 0.005STATE= RGBC Smooth_Th, 0.1STATE= HiDy Matrix, 1.6475 -0.7464 0.0989 -0.0636 1.0086 0.055 -0.0266 -0.8366 1.8632STATE= HiDy NR Noise Model Coef, 1STATE= HiDy PreWB Gb, 1STATE= HiDy PreWB Gr, 1STATE= HiDy TM Peak Percent, 0.003STATE= HiDy TM Sharp S, 2STATE= Gain Table, (null)](http://harvestimaging.com/blog/wp-content/uploads/2015/08/next_blog_21-300x191.jpg)
![// Captured 10:15:02 - Tuesday, August 25, 2015//// Frame 1 of 10 frames// Sensor info:// Width = 752// Height = 480// Image Format = Bayer 10// Subformat = BGGR// Sensor output = 10 bits per pixel//// .TIF file (RGB 48Bpp)//// Application version info:// Application name = DevWare.exe// Application version = 3.1.0.21// Application type = 3.1-Beta8// Application date = 12/04/2009// Firmware version = D.28//// Camera info:// productID = 0x100D Version = 0xC1// productName = Aptina Imaging DEMO2X// transportName = USB 2.0// num_chips = 1// sensor->sensorName = MI-0351// sensor->versionName = REV4// sensor->sensorFileName = sensor_dataMT9V024-REV4.sdat//// Sensor Fuse info:// FuseID: 308F9B95DFB5246B// Revision: 4// Silicon Option: --// // Windows OS info:// Display resolution = 1440x900 at 32bpp// OS Versioninfo = (5, 1, 2600, 2, Service Pack 2, 2, 0)// Microsoft Windows XP // Service Pack 2//// Processor info:// 1828 MHz// GenuineIntel// Intel(R) Core(TM)2 CPU T5600 @ 1.83GHz// 39 percent of memory is in use.// Memory 1014 MB (total)// Memory 608 MB (available)// Intel Pentium III//// USB 2.0 Enhanced Host Controllers:// Service: usbehci// Driver File: C:WINDOWSsystem32DRIVERSusbehci.sys// File Version: 5.1.2600.2180// Device Desc: Standard Enhanced PCI to USB Host Controller//// Aptina Imaging Camera Driver Info:// Service: MIUSB2// Driver File: C:WINDOWSSystem32Driversmiusb2.sys// File Version: 5.1.0.3508// Found Device: Vid_0634&Pid_100d// Service CYUSB not found// Service CYUSB not found[ColorPipe State]STATE= Display Zoom, 13STATE= Display Zoom Percent, 100STATE= Master Clock, 13500897STATE= Update Sensor FPS, 0STATE= Allow Update Sensor FPS, 1STATE= BitDepth, 10STATE= Filter, 3STATE= X Offset, 0STATE= Y Offset, 1STATE= Auto Offset, 1STATE= CFA Pattern, 0STATE= RGBC BiWindow, 2STATE= Monochrome, 1STATE= True Black Enable, 0STATE= True Black Level, 42STATE= Auto Luma Range, 1STATE= Luma Lo, 0STATE= Luma Hi, 255STATE= Unswizzle Mode, 3STATE= Swap 12-bit LSBs, 0STATE= Deinterlace Mode, 3STATE= Output Channel, 0STATE= Output BwColor, 0STATE= sRGB Color Standard, 0STATE= Color Correction, 0STATE= Gamma, 9STATE= Black Correct, 5STATE= Saturation, 10STATE= Contrast, 25STATE= Aperture Enable, 0STATE= Aperture, 5STATE= Black CCM Kill Enable, 0STATE= Black CCM Kill A, 240STATE= Black CCM Kill B, 160STATE= Black CCM Kill C, 80STATE= Green Balance Enable, 0STATE= Green Balance Apos, 128STATE= Green Balance Bpos, 10STATE= Green Balance Aneg, -128STATE= Green Balance Bneg, 10STATE= Auto Exposure, 0STATE= Auto Exposure Target, 50STATE= Auto Exposure Stability, 6STATE= Auto Exposure Speed, 30STATE= Auto Exposure Minimum FPS, 5STATE= Auto Exposure Flicker Filter, 0STATE= Auto Exposure Soft Limit, 33STATE= Auto Exposure Soft Gain Limit, 40STATE= Auto Exposure Software Gain Limit, 100STATE= Auto Exposure Freeze Gains, 0STATE= Auto Exposure Fade Saturation, 1STATE= Auto Exposure Fade Aperture, 1STATE= Auto Exposure Fade Target, 1STATE= Auto Exposure Inner Zone, 50STATE= Auto Exposure Outer Zone, 50STATE= Software Gain, 1000STATE= Mechanical Shutter Same, 1STATE= Mechanical Shutter Time, 33333STATE= Mechanical Shutter Delay, 0STATE= White Balance, 3STATE= WB Speed, 15STATE= WB Adjust Gains, 0STATE= WB Manual Position, 40STATE= WB Manual RedGreen, 100STATE= WB Manual BlueGreen, 100STATE= WB Interpolate Saturation, 1STATE= WB Normalize Matrix, 1STATE= AWB Weight Map Method, 0STATE= AWB Weight Map X Scale, 0STATE= AWB Weight Map Y Scale, 0STATE= AWB Weight Map X Shift, 0STATE= AWB Weight Map Y Shift, 0STATE= AWB Weight Map X Center, 0STATE= AWB Weight Map Y Center, 0STATE= AWB Weight Map Angle Sin, 0STATE= AWB Weight Map Angle Cos, 0STATE= AWB Weight Map Luma Low, 0STATE= AWB Weight Map Luma High, 0STATE= Minimum Gain, 1000STATE= Show Min Gain As 1, 1STATE= Default Relative Red Gain, 1000STATE= Default Relative Blue Gain, 1000STATE= Relative Red Gain, 1000STATE= Relative Blue Gain, 1000STATE= Lens Correction Enable, 0STATE= Lens Correction Falloff, 100STATE= Lens Correction Overlay, 0STATE= Lens Correction Center X, 376STATE= Lens Correction Center Y, 240STATE= Lens Correction Coeff Prec, 16STATE= Lens Correction Wide Angle, 0STATE= Lens Center Red X, 376STATE= Lens Center Red Y, 240STATE= Lens Center Green1 X, 376STATE= Lens Center Green1 Y, 240STATE= Lens Center Green2 X, 376STATE= Lens Center Green2 Y, 240STATE= Lens Center Blue X, 376STATE= Lens Center Blue Y, 240STATE= Lens Center Overlay, 0STATE= Lens Sim Sensor, 0STATE= Lens Sim Sensor Rev, 0STATE= Lens Sim Enable Pwq, 0STATE= Lens Sim Enable Poly, 0STATE= Noise Removal, 0STATE= Noise Removal Level, 25STATE= Noise Removal K1, 2000STATE= Noise Removal K2, 1800STATE= Noise Removal K3, 1000STATE= Noise Removal Edges, 1STATE= Noise Removal Kernel, 0STATE= HiDy 14bits, 0STATE= HiDy NR Enable, 0STATE= HiDy PreWB Autogain, 1STATE= HiDy TM Apply S-Curve, 1STATE= HiDy TM Enable LTM, 1STATE= Defect Enable, 0STATE= Defect Max, 1000STATE= Defect Auto Defect Correction, 0STATE= Flash Lamp, 0STATE= Still Global Reset, 0STATE= Global Reset Bulb, 0STATE= Num Capture Frames, 10STATE= Still Mode, 1STATE= Still Capture Average, 0STATE= Still Capture Timeout, 5STATE= Delay before snap, 0STATE= Save 24bpp BMP, 0STATE= Save RAW, 0STATE= Save TXT, 0STATE= Save HEX, 0STATE= Save ITX, 0STATE= Save RAW TIFF, 0STATE= Save 48bpp COLOR TIFF, 1STATE= Save JPEG, 0STATE= Save RAW JPEG, 0STATE= Save BMP Info, 0STATE= JPEG Quality (1-100), 100STATE= Save RAW PNG, 0STATE= Save PNG, 0STATE= Save DNG, 0STATE= Save Selection Rectangle, 0STATE= ICC Profile, 0STATE= Video Screen Capture, 1STATE= RAM Capture, 0STATE= RAM Capture MB, 512STATE= RAM Capture Cycle, 1STATE= WB Xenon Red Gain, 1024STATE= WB Xenon Blue Gain, 1024STATE= WB Led Red Gain, 1024STATE= WB Led Blue Gain, 1024STATE= MAE Overlay, 0STATE= Noise Image Type, 0STATE= Noise Frames, 50STATE= Strip FSP, 1STATE= Thumbnail Overlay, 1STATE= Check Thumbnail Table, 0STATE= CRA Overlay, 0STATE= Allow FAR Access, 1STATE= Pure Raw, 0STATE= AWB Incandescent, 1.3 -0.11 -0.18 -0.47 2.03 -0.49 -0.86 -0.79 5.66STATE= AWB Sun, 2.13 -0.09 -0.15 -0.44 2.09 -0.5 -0.1 -0.31 1.97STATE= AWB Incandescent Gain, 1 1STATE= AWB Sun Gain, 1 1STATE= WB Custom, 1 0 0 0 1 0 0 0 1STATE= WB Custom Xenon, 1 0 0 0 1 0 0 0 1STATE= WB Custom Led, 1 0 0 0 1 0 0 0 1STATE= AWB Weight Map, 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0STATE= Lens Curve Red, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= Lens Curve Green1, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= Lens Curve Green2, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= Lens Curve Blue, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= RGBC Sigma_S, 1STATE= RGBC Sigma_I, 0.005STATE= RGBC Smooth_Th, 0.1STATE= HiDy Matrix, 1.6475 -0.7464 0.0989 -0.0636 1.0086 0.055 -0.0266 -0.8366 1.8632STATE= HiDy NR Noise Model Coef, 1STATE= HiDy PreWB Gb, 1STATE= HiDy PreWB Gr, 1STATE= HiDy TM Peak Percent, 0.003STATE= HiDy TM Sharp S, 2STATE= Gain Table, (null)](http://harvestimaging.com/blog/wp-content/uploads/2015/08/next_blog_31-300x191.jpg)
![// Captured 10:20:13 - Tuesday, August 25, 2015//// Frame 1 of 10 frames// Sensor info:// Width = 752// Height = 480// Image Format = Bayer 10// Subformat = BGGR// Sensor output = 10 bits per pixel//// .TIF file (RGB 48Bpp)//// Application version info:// Application name = DevWare.exe// Application version = 3.1.0.21// Application type = 3.1-Beta8// Application date = 12/04/2009// Firmware version = D.28//// Camera info:// productID = 0x100D Version = 0xC1// productName = Aptina Imaging DEMO2X// transportName = USB 2.0// num_chips = 1// sensor->sensorName = MI-0351// sensor->versionName = REV4// sensor->sensorFileName = sensor_dataMT9V024-REV4.sdat//// Sensor Fuse info:// FuseID: 308F9B95DFB5246B// Revision: 4// Silicon Option: --// // Windows OS info:// Display resolution = 1440x900 at 32bpp// OS Versioninfo = (5, 1, 2600, 2, Service Pack 2, 2, 0)// Microsoft Windows XP // Service Pack 2//// Processor info:// 1828 MHz// GenuineIntel// Intel(R) Core(TM)2 CPU T5600 @ 1.83GHz// 39 percent of memory is in use.// Memory 1014 MB (total)// Memory 608 MB (available)// Intel Pentium III//// USB 2.0 Enhanced Host Controllers:// Service: usbehci// Driver File: C:WINDOWSsystem32DRIVERSusbehci.sys// File Version: 5.1.2600.2180// Device Desc: Standard Enhanced PCI to USB Host Controller//// Aptina Imaging Camera Driver Info:// Service: MIUSB2// Driver File: C:WINDOWSSystem32Driversmiusb2.sys// File Version: 5.1.0.3508// Found Device: Vid_0634&Pid_100d// Service CYUSB not found// Service CYUSB not found[ColorPipe State]STATE= Display Zoom, 13STATE= Display Zoom Percent, 100STATE= Master Clock, 13500897STATE= Update Sensor FPS, 0STATE= Allow Update Sensor FPS, 1STATE= BitDepth, 10STATE= Filter, 3STATE= X Offset, 0STATE= Y Offset, 1STATE= Auto Offset, 1STATE= CFA Pattern, 0STATE= RGBC BiWindow, 2STATE= Monochrome, 1STATE= True Black Enable, 0STATE= True Black Level, 42STATE= Auto Luma Range, 1STATE= Luma Lo, 0STATE= Luma Hi, 255STATE= Unswizzle Mode, 3STATE= Swap 12-bit LSBs, 0STATE= Deinterlace Mode, 3STATE= Output Channel, 0STATE= Output BwColor, 0STATE= sRGB Color Standard, 0STATE= Color Correction, 0STATE= Gamma, 9STATE= Black Correct, 5STATE= Saturation, 10STATE= Contrast, 25STATE= Aperture Enable, 0STATE= Aperture, 5STATE= Black CCM Kill Enable, 0STATE= Black CCM Kill A, 240STATE= Black CCM Kill B, 160STATE= Black CCM Kill C, 80STATE= Green Balance Enable, 0STATE= Green Balance Apos, 128STATE= Green Balance Bpos, 10STATE= Green Balance Aneg, -128STATE= Green Balance Bneg, 10STATE= Auto Exposure, 0STATE= Auto Exposure Target, 50STATE= Auto Exposure Stability, 6STATE= Auto Exposure Speed, 30STATE= Auto Exposure Minimum FPS, 5STATE= Auto Exposure Flicker Filter, 0STATE= Auto Exposure Soft Limit, 33STATE= Auto Exposure Soft Gain Limit, 40STATE= Auto Exposure Software Gain Limit, 100STATE= Auto Exposure Freeze Gains, 0STATE= Auto Exposure Fade Saturation, 1STATE= Auto Exposure Fade Aperture, 1STATE= Auto Exposure Fade Target, 1STATE= Auto Exposure Inner Zone, 50STATE= Auto Exposure Outer Zone, 50STATE= Software Gain, 1000STATE= Mechanical Shutter Same, 1STATE= Mechanical Shutter Time, 33333STATE= Mechanical Shutter Delay, 0STATE= White Balance, 3STATE= WB Speed, 15STATE= WB Adjust Gains, 0STATE= WB Manual Position, 40STATE= WB Manual RedGreen, 100STATE= WB Manual BlueGreen, 100STATE= WB Interpolate Saturation, 1STATE= WB Normalize Matrix, 1STATE= AWB Weight Map Method, 0STATE= AWB Weight Map X Scale, 0STATE= AWB Weight Map Y Scale, 0STATE= AWB Weight Map X Shift, 0STATE= AWB Weight Map Y Shift, 0STATE= AWB Weight Map X Center, 0STATE= AWB Weight Map Y Center, 0STATE= AWB Weight Map Angle Sin, 0STATE= AWB Weight Map Angle Cos, 0STATE= AWB Weight Map Luma Low, 0STATE= AWB Weight Map Luma High, 0STATE= Minimum Gain, 1000STATE= Show Min Gain As 1, 1STATE= Default Relative Red Gain, 1000STATE= Default Relative Blue Gain, 1000STATE= Relative Red Gain, 1000STATE= Relative Blue Gain, 1000STATE= Lens Correction Enable, 0STATE= Lens Correction Falloff, 100STATE= Lens Correction Overlay, 0STATE= Lens Correction Center X, 376STATE= Lens Correction Center Y, 240STATE= Lens Correction Coeff Prec, 16STATE= Lens Correction Wide Angle, 0STATE= Lens Center Red X, 376STATE= Lens Center Red Y, 240STATE= Lens Center Green1 X, 376STATE= Lens Center Green1 Y, 240STATE= Lens Center Green2 X, 376STATE= Lens Center Green2 Y, 240STATE= Lens Center Blue X, 376STATE= Lens Center Blue Y, 240STATE= Lens Center Overlay, 0STATE= Lens Sim Sensor, 0STATE= Lens Sim Sensor Rev, 0STATE= Lens Sim Enable Pwq, 0STATE= Lens Sim Enable Poly, 0STATE= Noise Removal, 0STATE= Noise Removal Level, 25STATE= Noise Removal K1, 2000STATE= Noise Removal K2, 1800STATE= Noise Removal K3, 1000STATE= Noise Removal Edges, 1STATE= Noise Removal Kernel, 0STATE= HiDy 14bits, 0STATE= HiDy NR Enable, 0STATE= HiDy PreWB Autogain, 1STATE= HiDy TM Apply S-Curve, 1STATE= HiDy TM Enable LTM, 1STATE= Defect Enable, 0STATE= Defect Max, 1000STATE= Defect Auto Defect Correction, 0STATE= Flash Lamp, 0STATE= Still Global Reset, 0STATE= Global Reset Bulb, 0STATE= Num Capture Frames, 10STATE= Still Mode, 1STATE= Still Capture Average, 0STATE= Still Capture Timeout, 5STATE= Delay before snap, 0STATE= Save 24bpp BMP, 0STATE= Save RAW, 0STATE= Save TXT, 0STATE= Save HEX, 0STATE= Save ITX, 0STATE= Save RAW TIFF, 0STATE= Save 48bpp COLOR TIFF, 1STATE= Save JPEG, 0STATE= Save RAW JPEG, 0STATE= Save BMP Info, 0STATE= JPEG Quality (1-100), 100STATE= Save RAW PNG, 0STATE= Save PNG, 0STATE= Save DNG, 0STATE= Save Selection Rectangle, 0STATE= ICC Profile, 0STATE= Video Screen Capture, 1STATE= RAM Capture, 0STATE= RAM Capture MB, 512STATE= RAM Capture Cycle, 1STATE= WB Xenon Red Gain, 1024STATE= WB Xenon Blue Gain, 1024STATE= WB Led Red Gain, 1024STATE= WB Led Blue Gain, 1024STATE= MAE Overlay, 0STATE= Noise Image Type, 0STATE= Noise Frames, 50STATE= Strip FSP, 1STATE= Thumbnail Overlay, 1STATE= Check Thumbnail Table, 0STATE= CRA Overlay, 0STATE= Allow FAR Access, 1STATE= Pure Raw, 0STATE= AWB Incandescent, 1.3 -0.11 -0.18 -0.47 2.03 -0.49 -0.86 -0.79 5.66STATE= AWB Sun, 2.13 -0.09 -0.15 -0.44 2.09 -0.5 -0.1 -0.31 1.97STATE= AWB Incandescent Gain, 1 1STATE= AWB Sun Gain, 1 1STATE= WB Custom, 1 0 0 0 1 0 0 0 1STATE= WB Custom Xenon, 1 0 0 0 1 0 0 0 1STATE= WB Custom Led, 1 0 0 0 1 0 0 0 1STATE= AWB Weight Map, 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0STATE= Lens Curve Red, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= Lens Curve Green1, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= Lens Curve Green2, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= Lens Curve Blue, C04037602403F800000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000STATE= RGBC Sigma_S, 1STATE= RGBC Sigma_I, 0.005STATE= RGBC Smooth_Th, 0.1STATE= HiDy Matrix, 1.6475 -0.7464 0.0989 -0.0636 1.0086 0.055 -0.0266 -0.8366 1.8632STATE= HiDy NR Noise Model Coef, 1STATE= HiDy PreWB Gb, 1STATE= HiDy PreWB Gr, 1STATE= HiDy TM Peak Percent, 0.003STATE= HiDy TM Sharp S, 2STATE= Gain Table, (null)](http://harvestimaging.com/blog/wp-content/uploads/2015/08/next_blog_41-300x191.jpg)