Harvest Imaging Blog

Over the last few years a lot of information about the Photon Transfer Curve (PTC) is being published in this blog.  The influence of many different sensor parameters on the PTC was studied and described.  For those of you that are still hungry to get more information, please remember that Jim Janesick wrote a complete book about the PTC.  It was Jim who developed this wonderful technique in the ‘80s for CCDs, but the PTC is perfectly applicable to CMOS imagers as well.  The great advantage of this measuring method is the fact that no absolute measurements of any light input is needed. 

In this blog, the application of the PTC on the data/images collected earlier will be described.  So the same images (with light on the sensor) as used in the previous blogs are being re-used.  What was done to generate these images : the sensor under test was uniformly exposed to light, while varying the exposure time.  For every exposure time applied, several images were grabbed, the average value of the obtained images as well as the temporal noise on pixel level was calculated. 

The measured signal of the sensor can be written as :

S_tot = kN_o + S_off    (1)

While the measured temporal noise on pixel level can be written as :

s_tot² = k²s_R² + k²s_o²  (2)

with :

–       S_tot : measured output signal [DN],

–       k : conversion gain [DN/e^–],

–       N_o : number of optically generated electrons,

–       S_off : offset signal [DN],

–       s_tot : total temporal noise measured [DN],

–       s_R : temporal noise associated with the readout channel [e^–], also the noise floor in dark at 0 s exposure time,

–       s_o : photon shot noise [e^–].

And with :

s_o² = N_o = (S_tot – S_off)/k       (3)

the total noise can be written as :

s_tot² = k²s_R² + k(S_tot – S_off).    (4)

The signal-to-noise ratio of the system under consideration can be written as :

                                    S_tot/s_tot = (S_tot-S_off)/( k²s_R² + k(S_tot – S_off))^0.5.     (5)

The obtained measurement data/images can be used to create :

1)    Standard deviation versus average effective signal, both on a log-scale (“Mean-Standard Deviation”).

 

The standard deviation is representing the temporal noise of the pixels, the effective signal is equal to the average output signal minus the DC-offset of the output signal.  The obtained curve is shown in Figure 1.

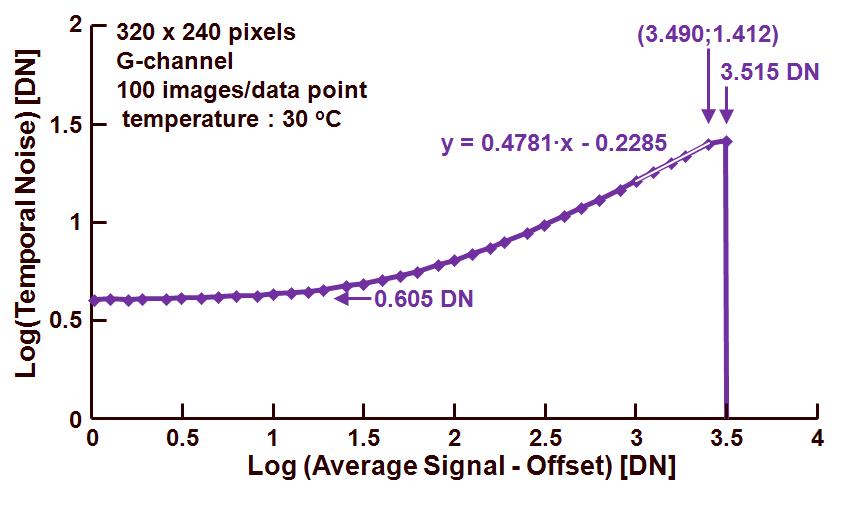
 Figure 1. Photon Transfer Curve : standard deviation versus effective output signal.

From left to right, one can recognize three parts in this PTC graph :

–       A flat part in which the temporal noise of the readout channel or the noise floor at 0 s exposure time, is dominant, in the example shown this noise is equal to 10^0.605 DN = 4.03 DN.  This can also be derived from equation (4) and scrapping the photon shot noise :

           s_tot² = k²s_R²    or    s_tot = ks_R.

–       A part with increasing noise for increasing effective signal, in this region the photon shot noise is dominant, and the slope of the curve needs to be equal to 0.5 (or at least very close to this value).  The regression line drawn through this part of the curve is characterized by the relation shown in the graph.  Using equation (4) again, but this time focusing on the photon shot noise, it reduces to :

 

    s_tot² = k(S_tot – S_off)    or    k = 1/(S_tot – S_off) at s_tot = 1 DN.

 

In this way the conversion gain k can be found by extrapolation of the regression line towards the crossing with the horizontal axis.  The value found for k is : 10^{-(0.2285/0.4781)} = 0.33 DN/e^–.  Be aware that this method actually requires the curve to get a slope = 0.5 before any extrapolation can be done.  In this example the slope is only 0.4781.  Although this value is pretty close to 0.5, a substantial error can be introduced into the calculation of the conversion factor.  For that reason a better method to find the conversion factor is in the “Mean-Variance” technique, explained further in this blog.

 

–       The part at which the noise reaches a maximum value and for any further increase in effective signal, the curve collapses.  This is the point at which the pixels reach their saturation level.  In the example shown, this happens for an effective output signal equal to 10^3.515 DN = 3273.0 DN.

 

2)    Variance versus average effective signal, both on a linear scale (“Mean-Variance”).

The curve obtained is illustrated in Figure 2.

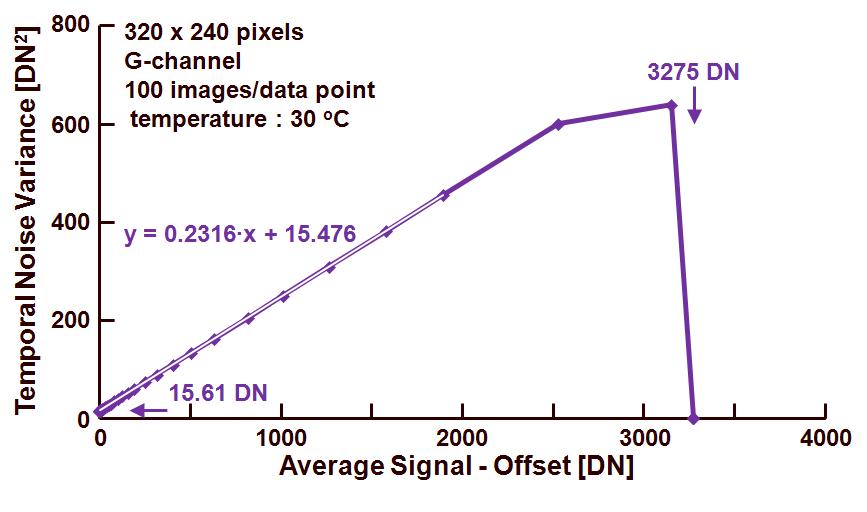
Figure 2. Photon Transfer Curve : noise variance versus effective output signal.

Also this figure shows some interesting features from left to right :

–       Crossing with the vertical axes (= 0 DN effective signal) for a noise variance equal to 15.61 DN.  This value corresponds to the temporal noise at very low signal values or noise floor in dark for 0 s exposure time, and actually should represent the variance of the noise associated with the readout channel.  The value found here is 15.61^0.5 DN = 3.95 DN.

 

–       A linear part in the curve for which the relation is shown in the figure.  In this region again formula (4) is valid :

     s_tot² = k²s_R² + k(S_tot – S_off).

 

Taking into account the relationship of the regression line, it should be concluded that the conversion gain k (being the slope of the line) is equal to 0.23 DN/e^–.  This value is lower than the one previously found with the Mean-Standard Deviation method.  This is due to the fact that there is a relative large error introduced in the calculation because the slope of the noise versus signal curve is not perfectly equal to 0.5 !

 

–       A saturation part with a collapsing curve for a maximum signal level of 3275 DN, being the saturation level of the pixels.

 

3)    Signal-to-noise ratio versus average effective signal, both on a log-scale (“Mean-Signal-to-Noise”).

The relation between signal-to-noise ration and effective signal is shown in Figure 3.

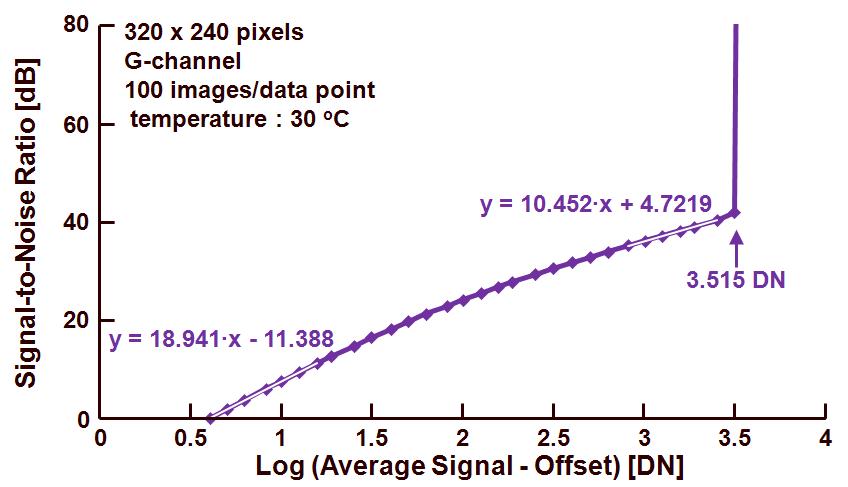 Figure 3. Photon Transfer Curve : signal-to-noise ratio versus effective output signal.

A similar story as before can be repeated about three different regions in the curve :

–       At the very left end a first part that can be linearized is indicated by the relation between signal-to-noise and average effective signal.  In this region the noise of the readout channel is dominant, and based on equation (5), the signal-to-noise ratio can be written as :

         S_tot/s_tot = (S_tot-S_off)/(ks_R)    or    ks_R=S_tot-S_off at S_tot/s_tot = 1.

In this example, the readout noise is equal to 10^{11.388/18.941} = 3.99 DN.

–       Just before saturation, a second linear part can be recognized in the region where the photon shot noise is the dominant noise source, and based on equation (5), the signal-to-noise ratio can be simplified to :

          S_tot/s_tot = ((S_tot-S_off)/k)^0.5    or    k = 1/(S_tot-S_off) at S_tot/s_tot = 1.

In this example, the conversion gain is equal to 10^{4.7219/10.452} = 0.35 DN/e^–.  Also this value deviates from the previously calculated values, because the extrapolation of the data can introduce some nasty errors.

–       Finally the signal-to-noise ratio is becoming extremely large, due to the fact that the temporal noise of the sensor is reduced to almost zero at saturation of the pixels for a value of 10^3.515 DN = 3273 DN.

In conclusion, parameters such as the readout noise or noise floor in dark, the conversion gain and the saturation level can be found by means of the Photon Transfer Curve.  But the most accurate and reliable data for (although 3 different curves are used, the input data for these curves is the same) :

–       the conversion gain can be obtained via the Mean-Variance curve,

–       the readout noise or noise floor in dark at 0 s exposure time, can be obtained via the Mean-Standard Deviation curve,

–       the saturation level can be obtained by any form of PTC.  

The PTC curve can be constructed in various ways.  In this blog uniform illuminated sensor areas at various exposure times are used, in the next blog a few alternatives will be highlighted.

Albert, 27-08-2012.

This entry was posted on Tuesday, August 28th, 2012 at 10:18 am and is filed under Uncategorized. You can follow any responses to this entry through the RSS 2.0 feed. You can leave a response, or trackback from your own site.