In the last blog the MTF measurement based on the slanted edge was introduced. As mentioned in that blog, to understand all ins and outs of the method, it is very beneficial to develop a small, simple model of the sensor with a slanted edge projected on it. And next, analyze the obtained, synthesized image. This simulation tool is also used here to check out the sensitivity of the technique w.r.t. the angle of the slanted edge.
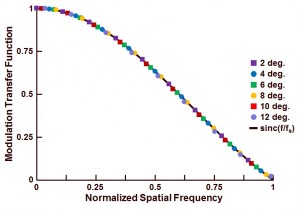
The result is shown in Figure 1.
Figure 1 : Effect of the slanted edge angle on the accuracy of the evaluation technique to characterize the MTF.
Shown are the MTF results obtained for a simulation of the angle being equal to 2 deg., 4 deg., 6 deg., 8 deg., 10 deg. and 12 deg. The ideal curve, obtained by the calculation of the sinc-function, is included as well. As can be seen from the curve :
- All evaluations based on an angle between 2 deg. and 10 deg. seem to fit very well to the ideal curve,
- The simulation result for an angle of 12 deg. shows some minor deviations from the ideal curve.
As a message from this simulation : angles of the slanted edge between 2 deg. and 10 deg. are very well suited for the MTF analysis. Once the angle is larger than 10 deg., the slanted edge method starts loosing its accuracy. The simulation results obtained here are fully in line with the advice of the ISO standard, which suggests also to use an angle of the slanted edge between 2 deg. and 10 deg.
Next time : how to implement oversampling and how to avoid aliasing effects during the measurements.
Albert, 04-07-2014.
Try 14.03624 degrees, and 26.565 degrees. Those correspond to slopes of 0.25 and 0.5 pixels respectively, and thus break the oversampling strategy of the slanted edge method.
Other than those two critical angles, you should be able to obtain decent results with anything between 0.5 degrees and 44.5 degrees.
For small angle you measure the MTF in the horizontal direction approximatively, which fits perfectly with the sinc function.
For big angles,you will start to measure the mtf in the diagonal direction, which is worse since the square photosite of the detector are “widder” on the diagonal.
@Fred: I agree with your statement that the photosite appears wider across the diagonal. This effect can be quite subtle in a real imaging system, i.e., after including aperture diffraction (http://mtfmapper.blogspot.com/2013/10/simulating-microlenses-first-take.html).
My original point still stands, though: the slanted edge method will measure the correct MTF even if the edge is at a 44 degree orientation — you will just have to replace the 1D sinc MTF with the appropriate cross-section taken from the 2D sinc MTF to obtain the reference MTF curve.
The reason, I suspect, for recommending angles between 2 and 10 degrees are twofold: a) it completely avoids the undersampling at the critical angles of 14 and 26 degrees, and b) it makes it simpler to remove the photosite aperture MTF if you want only the lens response (i.e., just divide by the appropriate 1D sinc).
Pretty! This was a really wonderful article.
Many thanks for supplying this info.