The MTF or Modulation Transfer Function can be measured in various ways. In the previous MTF-blogs the measurement by means of a Siemens Star testchart was discussed. This method has particular advantages, but also has some limitations, mentioned in earlier blogs. Another evaluation technique to characterize the MTF is based on the so-called slanted-edge method. Explained in words, this method sounds very complicated, but in reality it is really pretty simple.
There are several good references describing the slanted-edge method, e.g. :
- M. Estribeau and P. Magnan., in SPIE Proceedings, Vol. 5251, Sept. 2003,
- T. Dutton et al. in SPIE Proceedings, Vol. 4486, 2002, pp. 219-246,
- P.B. Burns, in Proceedings IS&T, 2000, pp 135-138,
- S.E. Reichenback et al. In Optical Engineering, pp. 170-177, 1991.
This slanted edge method became an ISO standard, namely ISO 12233. This is one of the very few ISO standards for image sensor and/or camera measurements.
The technique of the slanted edge can be described as follows :
- Image a vertically oriented edge (or a horizontal one for the MTF measurement in the other direction) onto the detector. The vertical edge needs to be slightly tilted with respect to the columns of the sensor. The exact tilting is of no importance, it is advisable to have a tilt of minimum 2o and maximum 10o w.r.t. the column direction. A tilt within these limits gives the best and most reliable results for the MTF characterization.
- Each row of the detector gives a different Edge Spread Function (ESF), and the Spatial Frequency Response (SFR) of the slanted edge can be “created” by checking the pixel values in one particular column that is crossing the imaged slanted edge.
- Based on the obtained SFR, the Line Spread Function (LSF) can be calculated, the LSF is simply the first derivative of the SFR.
- Next and final step is calculating the Fourier transform of the LSF. This results in the Modulation Transfer Function, because the MTF is equal to the magnitude of the optical transfer function, being the Fourier transform of the LSF. Plotting the MTF as a function of the spatial frequency can be done after normalizing the MTF to its DC component and normalizing the spatial frequency to the sampling frequency.
(In one of the coming blogs more info will be given on further improvement and/or sophistication of this procedure.)
A very helpful strategy in understanding how this MTF measurement method works and to check the algorithms, is to run a simulation and create an artificial image with a slanted edge that is sampled by an artificial sensor (e.g. with a pixel fillfactor of 100%). Next the theoretical, geometric MTF can be calculated as a sinc-function of the spatial frequency, while the synthetic image can be used as the input image to evaluate the MTF by means of the technique explained above (ESF, SFR, LSF, MTF). Such a simple simulation tool can also be used to check the influence of the various system parameters on the measurement technique. An example of such a simulation is shown in the following figures.
First of all a synthetic image is generated that results in a slanted edged of 4 deg. w.r.t. the column direction. A region-of-interest (ROI) of 200 (H) x 300 (V) pixels is created around the black-white transition of the slanted edge. This synthetic image is shown in Figure 1.
Figure 1 : ROI containing the slanted edge or black-white transition.
A particular column is selected (in this example column number 96), and all pixel values in this column are recorded to generate the SFR or Spatial Frequency Response. The result of this operation is shown in Figure 2, with reference to the left vertical axis.
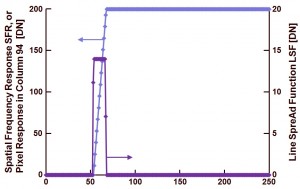Figure 2 : Spatial Frequency Response, being the values of the pixels present in column 96 of the image shown in Figure 1, and Line Spread Function, being the first derivative of the SFR.
Next the LSF or Line Spread Function is generated, simply by numerically calculating the first derivative of the SFR. The LSF is shown in Figure 2 as well, with reference to the right vertical axis.
Once the LSF is known, the magnitude of the FFT of this LSF is calculated. Plotting the FFT magnitude versus spatial frequency results in the MTF of the sensor, as shown in Figure 3. Notice that the MTF is normalized with its value a zero input frequency (= DC), while the spatial frequency is normalized to the spatial sampling frequency of the sensor. In this simulation example, the pixel pitch is equal to 6.5 µm.
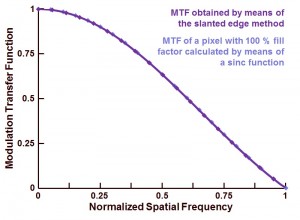Figure 3 : MTF of the simulated pixel (6.5 µm, 100 % FF), as well as the theoretical, geometric MTF of the same pixel.
In Figure 3 and next to the outcome of the MTF simulation, also the theoretical geometric MTF of the pixel is shown (6.5 µm, 100 % FF), for comparison reasons. This geometrical MTF is calculated by means of the well-known sinc-function. As can be seen, both curves coincide very nicely, indicating that the slanted edge method and the algorithms used in the calculation seem to do the job that they were developed for !
Before showing real measurements, in the next blog(s) a few additional improvements of the slanted edge method will be highlighted.
Albert, 18-06-2014.
It seems, this method can be used for area arrays only. Some applications do use linear arrays. For area arrays, this is equivalent to a simplified version of step-scanning a vertical slit. Time scanning is replaced by space scanning because so many rows of detectors are available.
This method can also be applied to linear imaging sensor also. However, it is limited to crossline direction.
Hello Albert,
I am currently trying to understand the MTF spatial frequency normalization. How does the pixel pitch correlate with the abscissa?
The pixel pitch defines the sample frequency. E.g. a pixel with a width of 5um, has 200 pixels/mm. That is becoming the spatial sample frequency. If the pixel gets smaller, the sample goes up, if the pixel gets bigger, the sample frequency is coming down. Half of the sample frequency is also known as the Nyquist frequency.
Hopefully this answers your question. Albert.
Hey Albert,
I have been struggling with calculating the MTF for 2/3 weeks. I am writing my own ray tracing code and i want to calculate the MTF my own optical system. I have tried few solution but none of them worked. Probably, i miss few theoretical information. So if you have any advice, i’d be happy.
By the way i read your article. There are very useful tricks that i will try on my code.
Hi, this is a difficult question. It is a bit the same as jumping in the water and then asking someone else to teach you how to swim …. I do need to know more details about what you are doing, otherwise I cannot help you.
Albert.
First of all thanks for quick response. I can deliver the details through e mail if it is possible. here is my mail: ecryildiz@gmail.com
At first i started with the ray trace algorithm. In a short of time, i succeed. then i thought i can go further. so i start to digging other optical problems. If i want to know my system’s optical quality, i have to know mtf curve so i can decide whether its high quality or not. But without image, i didn’t know how to find the mtf. so i propagate the rays through my system so i can obtain my spot diagram. I have been working 3-4 months about this subject but when it comes to write the codes i still couldn’t find out how to calculate the mtf. as i know, i have everything that i need to find the mtf except right formulas. before find diffraction limited mtf curves, i was looking for the geometrical mtf. but the formula that i found didnt work. this is my story 🙂
i’m waiting your mail. thanks for reply. have a great day.
Hello Albert,
I’m attempting to recreate your results above, but like others I’m struggling to plot against the normalized spatial frequency. I’ve chosen my sampling frequency to equal 2, since that is the number of pixels required to measure contrast. I’ve submitted a question on MATLAB Answers here 🙁https://www.mathworks.com/matlabcentral/answers/519124-fft-with-normalized-spatial-frequency), but perhaps you can quickly spot where I’ve gone wrong.
Appreciate the tutorial!
Ben
Hi Ben, You should chose a particular pixel pitch (e.g. 5 um), and this will define the sampling frequency. For a 5 um pixel pitch the sampling frequency is 200 pixels/mm.
Your suggestion of chosing the sample frequency equal to 2, means that you are working with pixels of 0.5 mm.
Success, Albert.
Thanks for the quick reply Albert! I’m afraid my issue must be something else. When I plot the resultant FFT I see 9 harmonics in the final frequency domain signal. The plot above indicates that the range of the MTF should be from the peak at DC to the first minimum (which makes sense). I’d be happy correspond over email if you’d like to see the plots. Or, you can see them at the link I shared above.
Thanks again for your help!
Ben
Hello Albert .
I am currently trying to calculate the mtf for an image of a phantom that has a resolution system up to 20 lp / mm. How can I get this graph, is it that I still don’t quite understand how to do it for several lines at different frequencies?
Hi, no idea what you are doing or whether you don’t understand what is going on …. ?
Do you want to calculate the mtf of a sensor with pixels of 2.5 um ?
Albert.
Hi Albert,
I did not find the disadvantages/limitations of the Siemens star method in your blog yet. Could you provide me that please?
If you don’t find it, then it is not there I guess.
Both have their pros and cons. Most important, the slanted edge is IEEE standardized, the Siemens Star is not (as far as I know). For both measurement techniques you do need dedicated software, I think the one for the Siemens Star is a bit easier to develop yourself.
Success, Albert.
Hi Albert,
How can I create an artificial image with a slanted edge that is sampled by an artificial sensor?
Please contact me off-line, I am not putting any simulation code on the blog.
Albert.
Hi Albert,
I would like to use the sampling frequency unit as lp/mm.
Then is the sampling frequency 200 pixels/mm equal to 100 lp/mm?
Hi, unfortunately your statement is not correct.
If you have 200 pixels/mm, you have a sample frequency of 200 pixels/mm or 200 linepairs/mm.
These 200 pixels/mm can resolve 100 linepairs/mm (every white line of a line pair covers 1 pixel and every black line of a line pair covers 1 pixel as well), so your statement is wrong.
Albert.
Hi Albert,
When we use image J to calculate MTF, if frequency units choose absolute lp/mm, what is the source of the following sensor size and number of photodetectors data? If I select 0, no data is output. If I choose relative cycles/pixel, I can output MTF data. What is the relationship between cycles/pixel and lp/mm?
thanks.
Hi, I am not familiar with the MTF module in imageJ. So I cannot give you answer to that question.
The metric lp/mm is an absolute one, the metric cycles/pixel is depending on the pixel size. So without knowing the pixel size, I do not know the ration between the two metrics.
Albert.
THANK YOU!