There is one important fixed-pattern noise component left in the discussion about how to measure the FPN with or without light input, being the FPN at saturation. These days most of the pixels have a built-in anti-blooming drain, e.g. lateral or vertical anti-blooming in CCDs or anti-blooming via the reset transistor in CMOS devices. In all cases the anti-blooming characteristics of the pixels is relying on a “parasitic” transistor that opens at the moment that the pixel is going into saturation. Because all these “parasitic” transistors differ in threshold voltage, all pixels have different anti-blooming characteristics, resulting in a (large) FPN component at saturation. To measure this component of the FPN, the devices need to be driven into saturation, and the variation along the pixels can be characterized. By itself, this is a very simple measurement.
Figure 1 shows the output characteristics of an imager (= average output signal of all green pixels) as a function of the exposure or integration time. The input settings are indicated in the figure.

Figure 1 : Average output signal of all green pixels as a function of the exposure time.
In Figure 1, three curves can be recognized, respectively for a setting of the on-chip analog amplifier equal to 2, 1 and 0.5. As can be seen, the curves for a gain equal to 2 and 1 saturate at 4095 DN. This indicates that the ADC is determining the saturation level of the signal and not the pixels themselves. The situation is different for a gain equal to 0.5. In that case the saturation level is within the range of the ADC, indicating that the sensor itself is saturating and not the ADC. In this example, the saturation at a gain equal to 0.5, is 2963 DN.
Of interest is the behavior of the FPN as a function of the same exposure time, as shown in Figure 2. Before calculation of the FPN, the defect pixels were removed from the data set, otherwise the defects will influence the measurement results to a large extend.
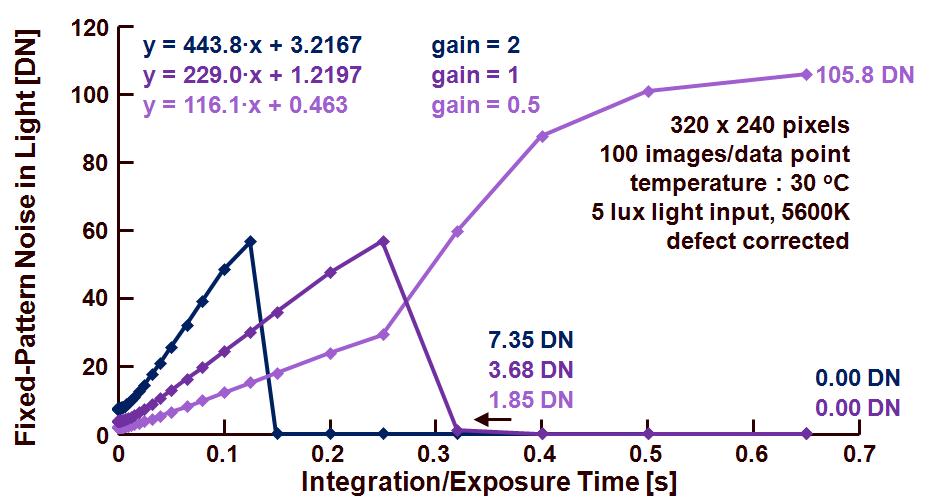
Figure 2 : FPN as a function of the exposure time.
As was the case in Figure 1, also here the FPN behaves differently depending on whether the ADC or whether the sensor is determining the saturation level. Two major cases can be distinguished :
– When the ADC determines the saturation level (for gain equal to 2 and 1) : the FPN initially increases in absolute value because of the PRNU, reaches a maximum and then collapses to reach a level of 0 DN. The latter refers to the fact that the saturation level of the ADC does not introduce any FPN in the case of saturation (apparently this example is using a sensor with a single ADC on-chip),
– When the sensor itself determines the saturation level (for gain equal to 0.5) : the FPN initially increases as well, due to the PRNU, but after a first linear increase, the FPN jumps to a very large value around 105.6 DN. For exposure times greater than 0.25 s, more and more pixels are saturating and more and more pixels contribute to a large FPN value generated by the anti-blooming transistors. As can be seen, the final value of the FPN in saturation is 105.6 DN, being equal to 105.6/(2963 – 819) = 4.94 % of the pixel saturation value.
Finally the FPN versus average signal is shown in Figure 3, the figure summarizes both curves already shown in the two previous ones.
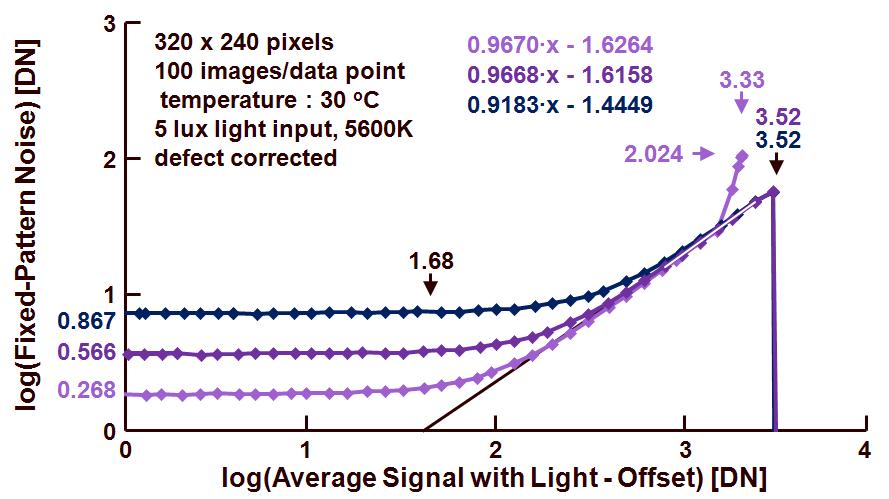
Figure 3 : FPN versus average signal for various settings of the analog gain.
From this curve the following data can be extracted :
– FPN in dark for the various gain settings is respectively 100.867 = 7.36 DN, 100.566 = 3.68 DN and 100.268 = 1.85 DN,
– The PRNU, independent of the gain setting, is equal to 10-1.68 or 0.0209 = 2.09 %,
– Saturation level is equal to 103.52 = 3311 DN for the gain equal to 2 or 1, and saturation level is equal to 103.33 = 2138 DN for a gain = 0.5,
– In the latter case the FPN at saturation is equal to 102.024 = 105.6 DN or 4.94 % while for the other gain settings, the FPN at saturation is equal to 0 DN.
That concludes the discussion on measuring fixed-pattern noise(s), in dark and with light on the sensor. Next time the measurement of the temporal noise components will start.
Albert, 01-05-2012.