Previous time it was explained that larger angles of the slanting edge may result in deviating MTF values. The results already presented in the previous post is repeated here in Figure 1.
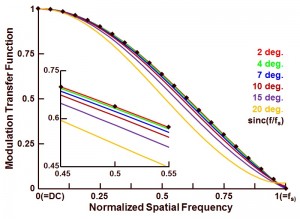Figure 1 : Effect of the slanted edge angle on the accuracy of the evaluation technique to characterize the MTF.
As a message from the simulation results shown in Figure 1 : angles of the slanted edge between 2 deg. and 10 deg. are very well suited for the MTF analysis. This can be seen by checking their comparison to the ideal curve (see black dots in Figure 1). Once the angle is larger than 10 deg., the slanted edge method starts loosing accuracy. The simulation results obtained here are fully in line with the advices of the ISO standard, which suggests also to use an angle of the slanted edge between 2 deg. and 10 deg. Just to highlight the deviations, an extra insert is included in Figure 1 to shown the MTF behaviour around the Nyquist frequency.
One of the reasons why angles larger than 10 deg. give deviating results is the fact that the number of measurement points in a particular sensor column is getting smaller and smaller if the angle is getting larger. This can indeed result in nasty effects on the MTF values and can lead to aliasing effects in the sampling of the data. To avoid these type of issues, it is possible to take the data of multiple columns into account instead of using the data of just a single column. To show the overall working principle of oversampling, the spatial frequency responses (SFR) of 4 neighbouring columns are shown before (Figure 2) and after (Figure 3) multiplexing the data into a single SFR.
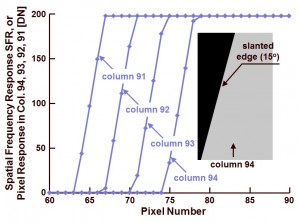Figure 2 : Spatial Frequency Response of 4 neighbouring columns.
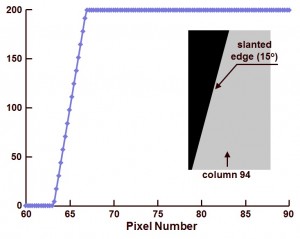
Figure 2 shows the data collected in 4 neighbouring columns, respectively columns 94, 93, 92 and 91, running vertically and crossing the slanted edge (which has an angle of 15 deg.). Four SFRs are obtained, all with a relative low amount of data points. As illustrated in Figure 3, the amount of data points can be increased by means of multiplexing the 4 curves of Figure 2 into one single SFR with 4 times the amount of samples.
Figure 3 : Spatial Frequency Response of the 4-times oversampled data, after multiplexing the 4 curves shown in Figure 2.
Based on this method of 4-times oversampling (also recommended by ISO 12233), the accuracy of the MTF measurement as a function of the angle of the slanted edge is checked again. The results of this exercise are shown in Figure 4.
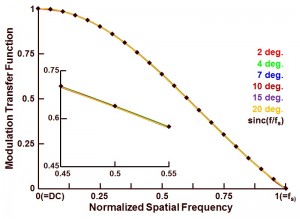
Figure 4 : Effect of the slanted edge angle on the accuracy of the evaluation technique to characterize the MTF, based on a 4-times oversampling of the SFR data.
The result is quite remarkable : up to an angle of 20 deg. no deviation between the various obtained MTF curves can be seen, even not in the insert showing the MTF around the Nyquist frequency.
So oversampling when obtaining the SFR is absolutely recommendable, because it results in more data points to generate the SFR. And in the simulation result described in this and previous blogs, the “measured” modulation transfer function does not deviate from the theoretical one.
Albert, 01-08-2014.
Hi Albert,
When trying to work it out analytically the effect of increasing angle on the MTF scales like sinc(0.5*tan(angle)) with sinc(x) as defined by Woodward.
Do you find this relationship back in the measurements?
Best regards,
Bert
This is very neat! I would’ve thought other effects related to the angle of the edge in relation to the pixel distribution would have been the cause, but it looks like only undersampling was the issue as you suggested and demonstrated! Thank you!
Hello Albert,
This ” method of 4-times oversampling (also recommended by ISO 12233)”, is it determined by the angle of that slanted edge? Say, 1/tan(15°) ? 4 ?
No, this is totally independent of each other. You can also do an oversampling number different from 4, and you will see, it still works.
Albert.