After measuring the noise in dark on column level, it is important to check noise in dark on row as well. This discussion will be very much the same as the last one about column level noise. The row level noise can be calculated based on the same data/images used for the FPN in dark and for the noise in dark on pixel and column level. It is just a matter of applying the right order of statistical calculations. To evaluate the noise in dark on row level, all pixels in each row are averaged and next the rms value is calculate on these averaged row values. Once the noise for each row is known, the average value of all these rms values is calculated.
The result of this process is shown in Figure 1. Both the temporal noise on pixel level (previous blog) and the temporal noise on row level are shown as a function of integration time.
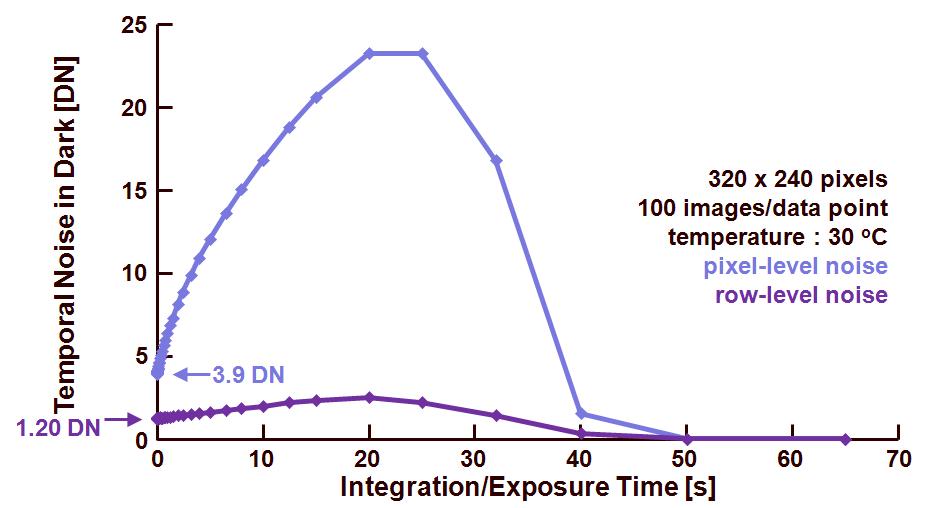
Figure 1. Temporal noise measured in dark on pixel level and on row level, as a function of the exposure or integration time.
As can be expected, the row level noise is much lower than the pixel level noise, the difference between the two curves is minimum at 0 s exposure time and at saturation. At lower exposure times, the temporal noise of the electronic circuitry plays an important role. For larger values of the exposure time, the dark shot noise is dominant and in that case, the averaging effect on the data removes this pixelized noise component. At saturation, the noise is reaching its minimum value.
Numbers that are obtained from this analysis :
– At 0 s exposure time, the temporal noise on row level is 1.20 DN,
– At 25 % of saturation, and for an exposure time of 8 s, the temporal noise on column level is 1.81 DN.
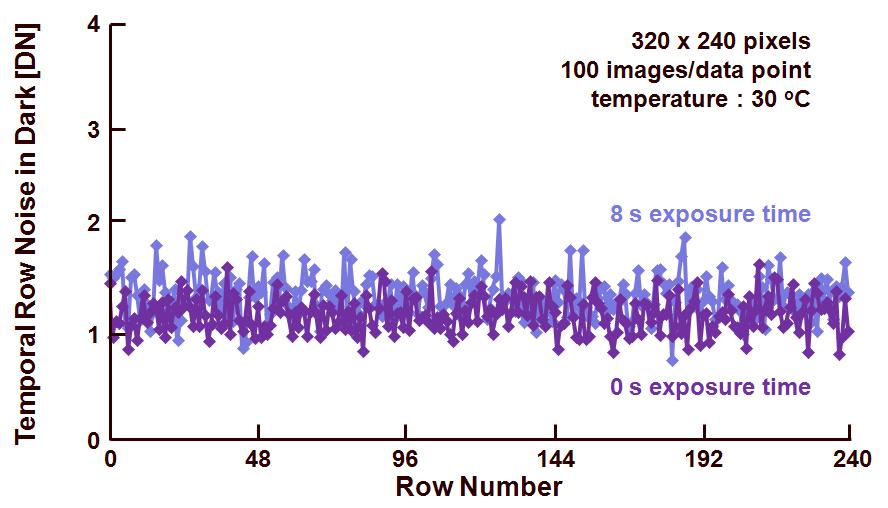
Figure 2. Temporal row noise (in dark) of the pixel at 0 s and 8s exposure time.
Figure 2 shows the row noise in dark for two integration times : 0 s (to get the noise without dark shot noise) and at 8s (when the pixels contain 25 % of the full well capacity). In both cases no repetitive pattern in the noise can be recognized, this is also verified by means of a FFT calculation. The result of this is shown in Figure 3.
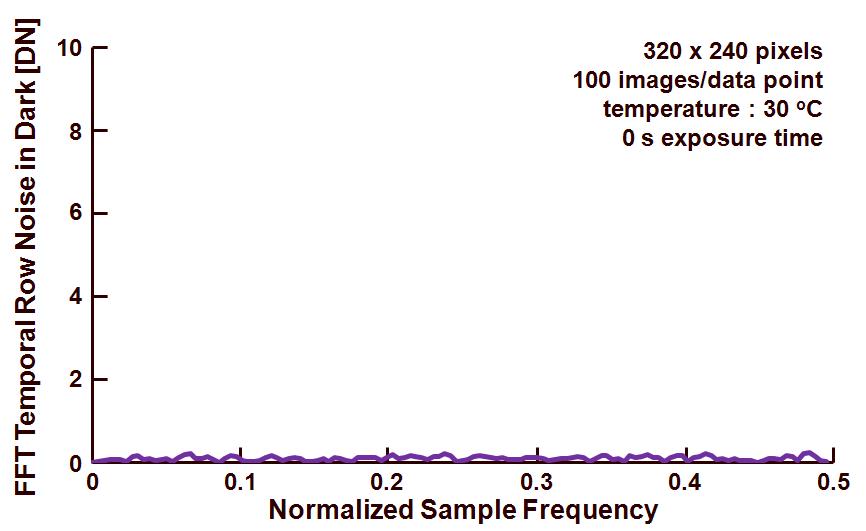
Figure 3. FFT of the row noise calculated for an exposure time of 0 s.
As can be observed in Figure 3, there is no specific FFT signal available at a particular frequency. From this one can conclude that the temporal row noise is randomly distributed.
Albert, 05-07-2012.
Albert,
one remark about the described method to measure row noise.
imagine an image of n rows and m columns,
pixel values being white gaussian noise of an RMS amplitude of X, and the noise being uncorrelated among the pixels.
Applying the method: create a vector of line averages and calculate the std deviation of the vector elements, gives a value which is greater than zero.
However, one will not recognize row noise in this image.
Now, would it not be reasonable to quadratically subtract the X/sqrt(m) contribution upfront and only name the rest “row noise” ?
hs
Heinrich, your idea is correct IF X is only pixel noise, and no column or row noise would exist. But you do not know upfront the pixel noise, what you measure is the total noise, including the row noise and the column noise !
Albert.